REVIEW OF ELEMENTARY REACTION KINETICS

We will briefly review various reaction orders for noncatalyzed reactions.

First Order Reaction:  

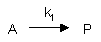
where k₁ is the first order rate constant.  For these reactions, the velocity of the reaction, v, is directly proportional to [A], or 

1.  v = -d[A]/dt = +d[P]/dT = k₁[A].  

The following differential equation can be written and solved to find [A] as a function of t.

-dA/dt = k₁[A]    or   dA/A = -k₁dt

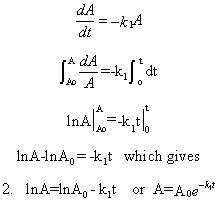
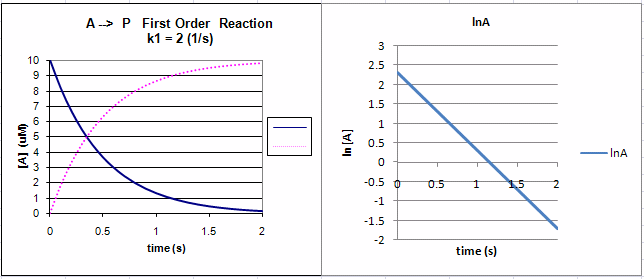
The following graphs show plots of A vs t and lnA vs t for data from a first order process.   Note that the derivative of the graph of A vs t (dA/dt) is the velocity of the reaction.  The graph of lnA vs t is linear with a slope of -k₁.  Note that the velocity of the reaction (slope of the A vs t curve) decreases with decreasing A, which is consistent with equation 1.  

Figure:  First Order Reaction:  A --> P

Second Order/Pseudo First Order Reactions

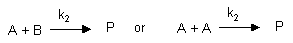
where k₂ is the second order rate constant.  For the first of these irreversible reactions, the velocity of the reaction, v, is directly proportional to [A] and [B], or 

3.  v = -d[A]/dt = -d[B]/dt =+d[P]/dT = k₂[A][B].  

We will consider two special cases of this reaction type:

• [B] >> [A].  Under these conditions, [B] never changes, so equation (3) becomes

4.  v = (k₂[B]) [A] = k₁' [A] 

where k₁' is the pseudo first order rate constant  (= k₂[B] ) for the reaction.  The reaction appears to be first order, depending only on [A].

• The only reactant is A which must collide with another A to form P, as illustrated in the second reaction above.  The derivations below apply to this special case.

The following differential equation can be written and solved to find [A] as a function of t.

5.  v = -d[A]/dt = +d[P]/dT = k₂[A][A] = k₂[A]² 

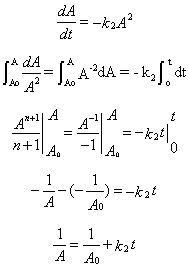
6.  1/A = 1/A_o  +  k₂t   

The following graphs show plots of A vs t and 1/A vs t for data from a second order process. 

Figure:  Second Order Reaction:  A + A --> P

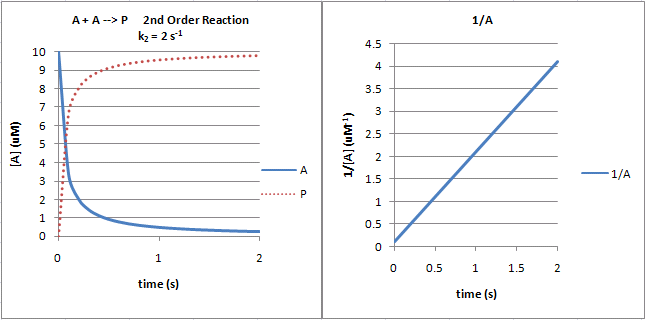
Note that just from a plot of A vs t, it would be difficult to distinguish a first from second order reaction.  If the plots were superimposed, you would observe that at the same concentration of A (10 for example as in the linked plots), the v_o of a first order reaction would be proportional to 10 but for a second order reaction to 10² or 100.  Therefore, the second order reaction is faster (assuming similarity in the relative magnitude of the rate constants) as indicated by the steeper negative slope of the curve.  However, at low A (0.1 example), the v_o of a first order reaction would be proportional to 0.1 but for a second order reaction to 0.1² or 0.01.  Therefore, the second order reaction is slower. 

Reversible First Order Reactions

A differential equation can be written for this reaction:

7.   v = -d[A]/dt = k₁[A] - k₂[P]

This can be solved through integration to give the following equations:

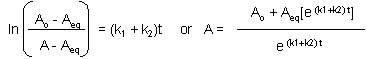
Graphs of A and P vs t for this reaction at two different sets of values of k₁ and k₂ are shown below.

Figure:  Reversible First Order Reactions:  A <=> P

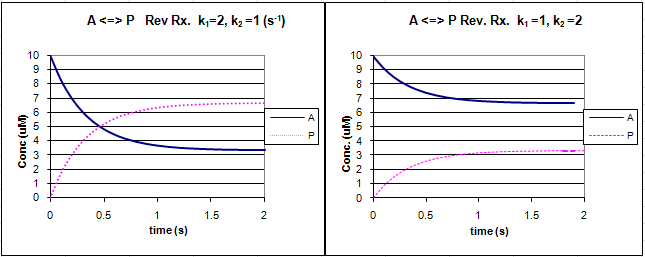
Go to the following spread sheet and change the values of k1 and k2.  Note the changes in the graphs.  Remember that the dissociation constant, Kd, is related to the rate constants by the formula Kd = k₂/k₁.  Note that if the first order rate constants are equal , Kd = Keq =1 and the equilibrium concentrations of A and P are equal.

Consecutive First Order Reactions

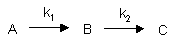
For these reactions:

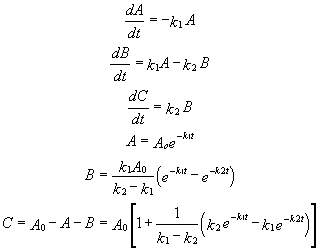
Graphs of A, B, and C vs t for these reaction at two different sets of values of k₁ and k₂ are shown below.

Figure:  Consecutive Irreversible First Order Reactions:  A --> B --> C

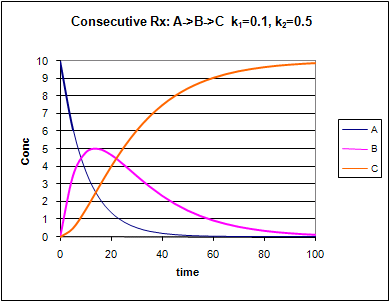
Change the values of k₁ and k₂.  Note the changes in the graphs. 

  Reactions Kinetics:  Java Applet  - Zero, First, and Second Order Reactions

Reaction Kinetics;  Java Applet - Change forward and reverse rate constants with graphical display.

We have previously derived equations for the reversible binding of a ligand to a macromolecule. Next we derived equations for the receptor-mediated facilitated transport of a molecule through a semipermeable membrane. This latter case extended the former case by the addition of a physical transport step. Now, in what hopefully will seem like deja vu, we will derive almost identical equations for the chemical transformation of a ligand, commonly referred to as a substrate, by an enzyme. Two scenarios will be studied.

1. Rapid Equilibrium Assumption - enzyme (macromolecule) and ligand (substrate) concentrations can be determined using the dissociation constant since E, S, and ES are in rapid equilibrium, as we previously used in our derivation of the equations for facilitated transport.
2. Steady State Assumption (more general) -  enzyme and substrate concentrations are not those determined using the dissociation constant.

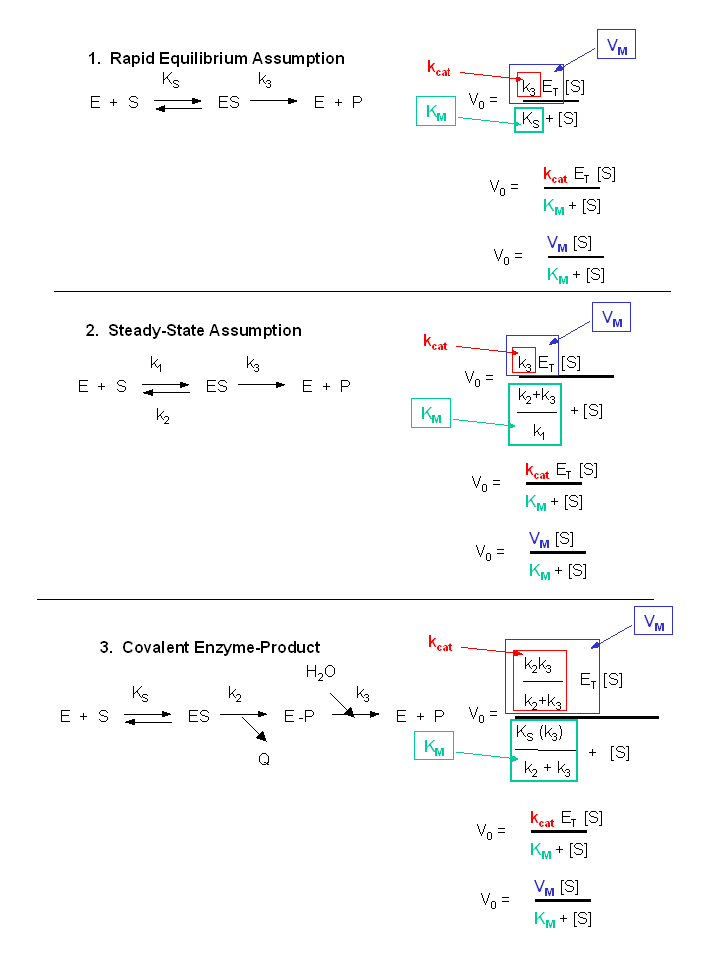
RAPID EQUILIBRIUM ASSUMPTION - HENRI-MICHAELIS-MENTEN EQUATION

Consider the following reaction mechanism for the enzyme-catalyzed conversion of substrate S into product P. (We will assume that the catalyzed rate is much greater than the noncatalyzed rate.)

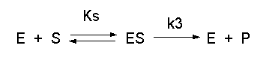
As we did for the derivation of the equations for the facilitated transport reactions under rapid equilibrium conditions, this derivation is based on the assumption that the relative concentrations of S, E, and ES can be determined by the dissociation constant, Ks, for the interactions and the concentrations of each species during the early part of the reaction (i.e. under initial rate conditions). Assume also the S >> E_o.  Remember that under these conditions, S does not change much with time. Is this a valid assumption?  Examine the mechanism shown above.  S binds to E with a second order rate constant k₁.  ES has two fates. It can dissociate with a first order rate constant k₂ to S + E, or it can be converted to product with a first order rate constant of k₃ to give P + E. If we assume that k₂ >> k₃ (i.e. that the complex falls apart much more quickly than S is converted to P), then the relative ratios of S, E, and ES can be described by Ks. Alternatively, you can think about it this way. If S binds to E, most of S will dissociate, and a small amount will be converted to P. If it does, then E is now free, and will quickly bind S and reequilibrate since the most likely fate of bound S is to dissociate, not be converted to P (since k₃ << k₂). This make sense also, if you consider that the physical step characterized by k₂ is likely to be quicker than the chemical step, characterized by k₃. Hence the following assumptions have been used:

• S >> E_o
• P_o = 0
• k₃ is rate limiting (i.e. the slow step)

Let's assume that for this system that the initial velocity will be measured. We would like to derive equations which show the initial velocity v_o as a function of the initial substrate concentration, S_o , (assuming that P is negligible over the time course of measuring the initial velocity). Also assume that the v _catalyzed >> v_noncatalyzed. In contrast to the first-order reaction of S to P in the absence of E, v is not proportional to S_o but rather to S_bound. as we described in class with facilitated diffusion (flux proportional to AR, not free A). Therefore,

v_o a ES, or

Equation 1)   v_o = v = const [ES] = k₃ [ES]

where v_o is the  initial velocity.   How can we calculate ES when we know S (which is equal to S_o) and E_tot (which is E_o)? Let us assume that S is much greater than E, as is the likely biological case. We can calculate ES using the following equations and the same procedure we used for the derivation of the binding equation, which gives the equation below:

ES = (E_oS)/(K_s + S)   (analogous to ML = (M_oL)/(K_d + L) 

DERIVATION

Equation 5)    v = const [ES] = k₃ [ES] = k₃ EoS/(Ks + S) = VmS/(Ks + S).

This is the world famous Henri-Michaelis-Menten Equation

It should be clear to you from this equation that:

• a plot of v vs S is hyperbolic
• v = 0 when S = 0
• v is a linear function of S when S<<Ks.
• v = V_max (or Vm) when S is much greater than Ks
• S = Ks when v = V_max/2.

These are the same conditions we detailed for our understanding of the binding equation

ML = (M_oL)/(K_d + L)

• History and Picture of Maude Menten

STEADY STATE ASSUMPTION

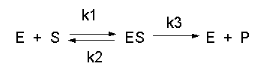
In this derivation, we will consider the following equations and all the rate constants, and will not arbitrarily assume that k₂ >> k₃. We  will still assume that S >> E_o and that P_o = 0. An added assumption, however, is that dES/dt is approximately 0. Look at this assumption this way. When an excess of S is added to E, ES is formed. In the rapid equilibrium assumption, we assumed that it would fall back to E + S faster than it would go onto product. In this case, we will assume that it might go on to product either less or more quickly than it will fall back to E + S. In either case, a steady state concentration of ES arises within a few milliseconds, whose concentration does not change significantly during the initial part of the reaction under which the initial rates are measured. Therefore, dES/dt is about 0. In the rapid equilibrium derivation, we observed that v = k₃ES.   We then solved for ES using Ks and mass balance of E. In the steady state assumption, the equation v = k₃ES still holds, but know we will solve for ES using the steady state assumption that dES/dt =0.

Equation 1)    v = k₃ES

Equation 6: (steady state) dES/dt = k₁(E)(S) - k₂(ES) -k₃(ES) = 0

k₁(E)(S) = (k₂ + k₃)(ES)

k₁(E_o-ES)(S) = (k₂ + k₃)(ES)

k₁(E_o)(S) - k₁(ES)(S) = (k₂ + k₃)(ES)

k₁(E_o)(S) = (k₂ + k₃)(ES) + k₁(ES)(S)

  k₁(E_o)(S) = ES (k₂ + k₃ + k₁S)

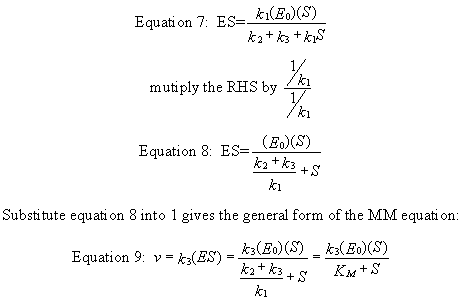
Equation 9)   v = k₃ES = [k₃(E_o)(S)]/ [(k₂ + k₃)/k₁ + S] = [k₃(E_o)(S)]/(K_m+ S)

ANALYSIS OF THE GENERAL MICHAELIS MENTEN EQUATION

This equation can be simplified and studied under different conditions. First notice that (k₂ + k₃)/k₁ is a constant which is a function of relevant rate constants. This term is usually replaced by K_m which is called the Michaelis constant. Likewise, when S approaches infinity (i.e. S >> K_m, equation 5 becomes v = k₃(E_o) which is also a constant, called V_m for maximal velocity. Substituting V_m and K_m into equation 5 gives the simplified equation:

Equation 10)   v = V_m(S)/(K_m+ S)

It is extremely important to note that Km in the general equation does not equal the Ks, the dissociation constant used in the rapid equilibrium assumption!    Km and Ks have the same units of molarity, however. A closer examination of Km shows that under the limiting case when k₂ >> k₃ (the rapid equilibrium assumption) then,

Equation 11)  Km = (k₂ + k₃)/k₁ = k₂/k₁ = Kd = Ks.

If we examine Equations 9 and 10 under several different scenarios, we can better understand the equation and the kinetic parameters:

• when S = 0, v = 0.
• when S >> Km, v = Vm = k₃E_o. (i.e. v is zero order with respect to S and first order in E. Remember, k₃ has units of s^-1since it is a first order rate constant. k₃ is often called the turnover number, because it describes how many molecules of S "turn over" to product per second.
• v = Vm/2, when S = Km.
• when S << Km, v = VmS/Km = k₃E_oS/Km (i.e. the reaction is bimolecular, dependent on both on S and E. k₃/Km has units of M^-1s^-1, the same as a second order rate constant.

Notice that equations 9 and 10 are exactly analysis to the previous equations we derived:

• ML = M_oL/(Kd + L) for binding of L to M
• J_o = J_mA/(Kd + A) for rapid equilibrium binding and facilitated transport of A
• v_o = VmS/(Ks + S) for rapid equilbirum binding and catalytic conversion of A to P.
• v_o = V_m(S)/(K_m+ S) for steady state binding and catalytic conversion of A to P.

Please notice that all these equations give hyperbolic dependencies of the y dependent variable (ML, J_o, and v_o) on the ligand, solute, or substrate concentration, respectively.

Java Applet:  Michaelis-Menten Plots

EQUATION FOR MORE COMPLICATED REACTION

Not all reactions can be characterized so simply as a simple substrate interacting with an enzyme to form an ES complex, which then turns over to form product. Sometimes, intermediates form. For example, a substrate S might interact with E to form a complex, which then is cleaved to products P and Q. Q is released from the enzyme, but P might stay covalently attached. This happens often in the hydrolytic cleavage of a peptide bond by a protease, when an activated nucleophile like Ser reacts with the sessile peptide bond in a nucleophilic substitution reaction, releasing the amine end of the former peptide bond as the leaving group, while the carboxy end of the peptide bond remains bonded to the Ser as an Ser-acyl intermediate. Water then enters and cleaves the acyl intermediate, freeing the carboxyl end of the original peptide bond. This is shown in the written reaction below:

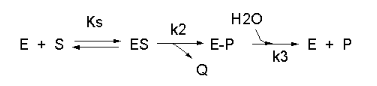
To simplify the derivation of the kinetic equation, let's assume that E, S, and ES are in rapid equilibrium defined by the dissociation constant, Ks. Assume Q has a visible absorbance, so it is easy to monitor.  Assume from the steady state assumption that:

d[E-P]/dt = k₂[ES] - k₃[E-P] = 0  (assuming k₃ is a pseudo first order rate constant and [H₂O] doesn't change.

The velocity depends on which step is rate limiting.  If k₃<<k₂, then the k₃ step is rate-limiting.   Then

  v = k₃[E-P]

  If k₂<<k₃, then the k₂ step is rate-limiting.  Then

  v = k₂[ES]

For a homework assignment, you derived the following kinetic equation for this reaction, assuming  v = k₂[ES].

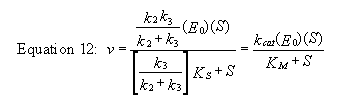
You can verify that you get the same equation if you assume that v = k₃[E-P].  (Also, k_cat will be defined below.)

This equation looks quite complicated, especially if you substitute for Ks, k_-1/k₁. All the kinetic constants can be expressed as functions of the individual rate constants. However this equation can be simplified by realizing the following:

• When S >> [Ks(k₃)/(k₂+k₃)], v = [(k₂k₃)/(k₂ + k₃)]E_o = Vm
• [Ks(k₃)/(k₂+k₃)] = constant = Km

Substituting these into equation 7 gives:

Equation 13 - v = V_m(S)/(K_m+ S)

This again is the general form of the Michaelis-Menten equation

Note in the first bulleted item above that for this reaction, Vm = [(k₂k₃)/(k₂ + k₃)]E_o

This is more complicated than our earlier definition of Vm = k₃E_o. They are similar in that the term E_o is multiplied by a constant which is itself a function of rate constant(s). The rate constants are generally lumped together into a generic constant called k_cat. For the simple reaction k_cat = k₃ but for the more complicated reaction with a covalent intermdiate which we just deived, k_cat = (k₂k₃)/(k₂ + k₃). For all reactions,

Equation 14 - Vm = k_catE_o.

Figure:  Summary of v_o vs S equations - Meanings of Km, k_cat and Vm.

• Km and k_cat values for various enzymes

• diffusion controlled enzymes

eXPERIMENTAL DETERMINATION OF V_m AND K_m 

How does one extract  V_m and  K_m  from experimental data?  We have already answered this question when we explored different mathematical transformations of the binding equation to determine Kd.  These included:

• nonlinear hyperbolic fit

• double reciprocal plot

• Scatchard plot

The double-reciprocal plot is commonly used to analyze initial velocity vs substrate concentration data.  When used for such purposes, the graphs are referred to as Lineweaver-Burk plots, where plots of 1/v vs 1/S are straight lines with slope m = K_M/V_max, and y intercept b = 1/V_max.  These plots can not be analyzed using linear regression, however, since that method assumes constant error in the y axis (in this case 1/v) data.  A weighted linear regression or even better, a nonlinear fit to a hyperbolic equation should be used.  The Mathcad template below shows such a nonlinear fit.  In the laboratory, we will use a series of programs developed by W. W. Cleland specifically designed to analyze initial rate data of enzyme catalyzed reactions.

Mathcad 8 - Nonlinear Hyperbolic Fit.  V_m and K_m.