So far we have studied molecular aggregates (micelles and bilayers) and macromolecular structure (mostly
proteins). Next we studied binding interactions which are the first steps in the expression of biological activity of
a macromolecule. For some proteins, reversible binding is their sole function (consider the binding of dioxygen to
myoglobin and hemoglobin). For many others, it is not. For those, what can happen next?
The answer to that question clearly depends on the biological function of the macromolecule. We
can simplify this process by adding one additional step as reflected in the equilibrium binding expression shown below:
M + L <==> ML <==> M + X
This expression indicates that the free ligand has changed in some fashion to x. In this chapter,
we will consider two kinds of transformations:
- L is a ligand on the outside of a biological membrane (Lout) which binds to a membrane protein
receptor, R. This undergoes a conformational change (as we studied in the binding of dioxygen to hemoglobin) which
leads to the expulsion of the bound ligand to the inside of the membrane (Lin). This can modeled with the
simple equation:
R + Lout <==> RL <==> R + Lin
. This process is called facilitated diffusion and represents a physical as opposed to chemical
process since no covalent bonds are made or broken. This process proceeds down a concentration or chemical potential
gradient (Dmo < 0) and hence is spontaneous (thermodynamically
favored). If the ligand concentration is higher inside the cell, net diffusion moves it to the outside of the cell.
Passive (non-facilitated) diffusion is kinetically slow in the absence of a receptor since membranes present formidable barriers
to the passage of polar molecules.
- L is a ligand (or substrate S) which binds to a protein enzyme, E. The bound substrate is
chemically altered to produce a new product, P, which dissociates from the enzyme. This can be expressed most simply
as:
E + S <==> ES <==> E + P .
This section will discuss diffusion processes. First, diffusion equations will be derived
for cases not involving a binding receptor. The equation will show the rate of diffusion of a solute across a membrane
from a region of high concentration to a region of low concentration (Dmo
< 0) is a linear function of [DL] across the membrane. Next we will
derive equations for receptor-mediated diffusion across a membrane - facilitated diffusion. We
will deal with the situation when the solute must be transported up a concentration gradient (which requires ATP as an exogenous
source of energy), a process called active transport, later in this web book.
PASSIVE DIFFUSION THROUGH A MEMBRANE - CASE 1: no receptor
 Java Applet: Before you study the derivation for simple passive diffusion, view the applets below. For some reason I
can't put a direct link in for them and still have the applets work. To get around it, I've put the files in the following
directories. Use the File, Open, the Browse button on your brower (Netscape or IE) to open them.
Java Applet: Before you study the derivation for simple passive diffusion, view the applets below. For some reason I
can't put a direct link in for them and still have the applets work. To get around it, I've put the files in the following
directories. Use the File, Open, the Browse button on your brower (Netscape or IE) to open them.
- Diffusion 20: chemgard$ on 'Reliant' (I) /Biochem/applets/diffusion/diffusion1.html
- Diffusion 40: chemgard$ on 'Reliant' (I) /Biochem/applets/diffusion40/diffusion40.html
- Diffusion 80: chemgard$ on 'Reliant' (I) /Biochem/applets/diffusion80/diffusion80.html
(Run each applet several times for 10 seconds and record the number of balls that pass through the membrane
to the right hand side. Graph that number versus the the initial number on the left hand side (20, 40, and 80, respectively,
for the files above).
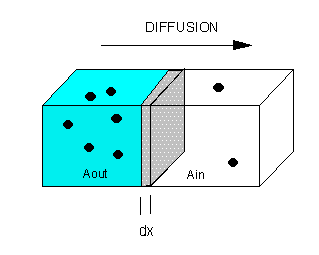
The flux of molecule A (JA) across a membrane of thickness dx, is proportional
to the concentration gradient across the membrane, dA/dx., which gives Fick's First Law of Diffusion:
JA a dA/dx
or JA= - D dA/dx
where D is the diffusion coefficient (cm2/s). The negative sign is necessary since concentration
increases in the opposite direction of net flux. For these derivations, we will assume the JA is the initial
flux. That is, the flux is measured for a short enough time that the relative concentrations of A on both sides of the membrane
does not change significantly. It should be clear that eventually the net flux levels off to zero, when the concentrations
of A on both sides of the membrane are equal (i.e. the chemical potential of A on both sides is identical).
This can also be expressed as JA = -L dmA/dx
, which bridges kinetic and thermodynamic aspects of diffusion.
For JA = - D dA/dx, dimensional analysis shows that
J = moles/area/sec = mol/cm2.s = - (cm2/s) mol/cm3/cm. Hence the units
of D are cm2/s.
Rearranging Fick's Law gives the following:
JA = - D dA/dx
òJA
dx = -DòdA
Integrate both sides with x varying btw 0 and x (the thickness of the membrane), and A from
A0 (A out) to Ai (A in)
JA x = -D [Ai - Ao] = D [A0 - Ai]
or
JA = (D/x) [A0 - Ai] or
JA = P [A0 - Ai]
where P is the permeability coefficient, which has units of cm2/s/cm or cm/s. (We discussed
permeability coefficients for different solutes traversing model bilayers when we discussed lipids.)
A plot of JA vs (A0 - Ai) is linear, with a slope of D/x
FACILITATED DIFFUSION THROUGH MEMBRANE - CASE 2: receptor-mediated.
Consider the following mechanism:
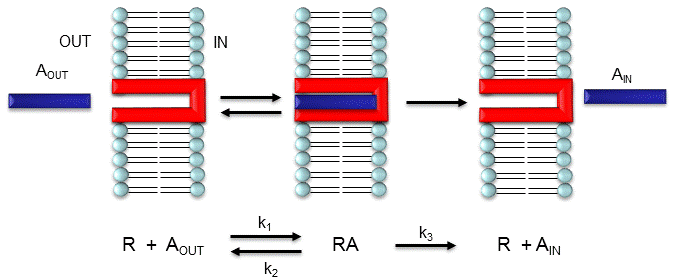
Let's assume that for this system the initial flux will be measured. We would like to derive equations
which show J as a function of Ao (assuming that Ai is negligible over the time course of measuring the
initial flux. Also assume that the J facilitated is much greater than J passive. In contrast to passive
diffusion, JA is not proportional to Ao but rather to [Abound].
Consider this example to help you with that concept. Pretend that the receptor is a truck which
can carry one particle across the membrane at a time (i.e. 1/1 stoichiometry). Also assume that the particle can't get across
without being carried by the truck. If there are no trucks in the membrane, no load can be delivered. If there
are trucks in the membrane but no particles in them, no load will be delivered. As the number of particles available
to be loaded into the truck increase, the truck will have an increased chance to be loaded (depending of course on the affinity
of the particle for the truck). If the number of loaded trucks is doubled, the number of particles dumped to the
other side will double. Therefore, by analogy,
JA is proportional to AR, or
Equation 1: JA = const [AR] = k3 [AR]
How can we calculate AR when when know A and R? Let us assume that A is much greater than R, as is the
likely biological case. We can calculate AR using the following equations, and the same procedure we used for the derivation
of the binding equation
ML = (MoL)/(Kd + L)
Equation 2 - Dissociation constant: K d = ([A]eq[R]eq)/[AR]eq = ([A][R])/[AR]
(units of molarity)
Equation 3 - Mass Balance of R: Ro = R + RA
Since we will assume that A is much greater than R, we will not need the mass balance for A (which is
Ao = A + AR)
Substitute 3 into 2:
(AR)Kd = (Ro)A - (AR)A
(AR)Kd + (AR)A = (Ro)A
Equation 4: AR = (Ro)A/(Kd + A)
Substitute 4 into 1 gives the final equation,
Equation 5: JA = const [AR] = k3 [AR] = k3 (Ro)A/(Kd
+ A).
It should be clear to you from this equations that:
- a plot of JA vs A is hyperbolic
- JA = 0 when A = 0.
- JA = Jmax when A is much greater than Kd
- A = Kd when JA = Jmax/2.
These are the same conditions we detailed for our understanding of the binding equation
ML = (MoL)/(Kd + L)
RAPID EQUILIBRIUM ASSUMPTION
This derivation is based on the assumption that the relative concentrations of A, R, and AR can be determined
by the Kd for the interactions and the concentrations of each species during the early part of diffusion (i.e. under initial
rate conditions). Remember under these conditions, Aout out does not change much with time. Is this
a valid assumption? Examine the mechanism shown in the above figure. Aout binds to R with a second
order rate constant k1. AR has two fates. It can dissociate with a first order rate constant k2 to Aout
+ R, or it can be carried across the membrane with a first order rate constant of k3 to give Ain + R.
If we assume that k2 >> k3 (i.e. that the complex falls apart much more quickly than A is carried
in), then the relative ratios of A, R, and AR can be described by Kd. Alternatively, you can think about it this way.
If A binds to R, most of A will dissociate, and a small amount will be carried across the membrane. If this happened, then
R is now free, and will quickly bind Aout and reequilibrate. This occurs since the most likely fate of bound
A is to dissociate, not to be carried in, since k3 << k2.
Diffusion of Ions and Molecules Across Membranes
As we saw previously, the permeability coefficients of synthetic membranes (liposomes) to solutes is related to the size and polarity of the solute.
Figure: permeability coefficients
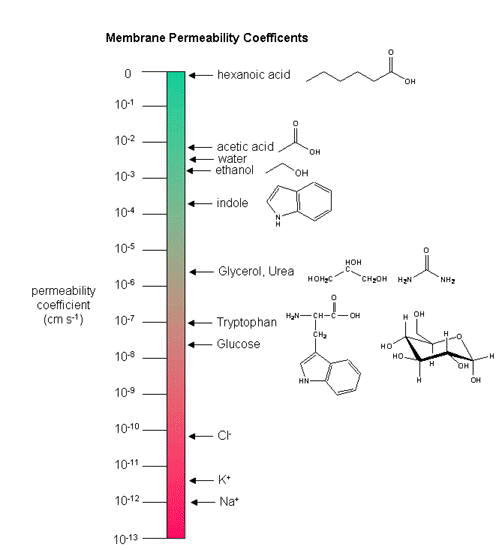
Smaller, higher charge density ions (like Na+) have a lower permeability coefficient than do
larger, lower charge density ions (like K+). What about natural membranes? Look at the chart
below.
Permeability coefficient (cm/s) of natural and synthetic membranes to D-Glucose
and D-mannitol at 25oC.
| Membrane Preparation |
D-Glucose |
D-Mannitol |
| Synthetic Lipid Bilayer |
2.4 x 10-10 |
4.4 x 10-11 |
| Calculated Passive Diffusion |
4 x 10-9 |
3 x 10-9 |
| Intact Human Erythrocyte (red blood cell) |
2.0 x 10-4 |
5 x 10-9 |
The anomalous data point is for diffusion of D-glucose into red blood
cells. This clearly indicates that the diffusion is not passive but facilitated by a receptor which can distinguish
it from a closely related substance, D-mannitol.
"Receptors" in Facilitated Diffusion
Two types of proteins are involved in facilitated diffusion. The type described best
by this section are carrier proteins (which are often called permeases or transport proteins).
The receptor referred to above that moves glucose across the membrane is a glucose transporter (GLUT1). The other type
that facilitate diffusion of ions down a concentration gradient are called channels. In the former cases, the
ligand binds the receptor (permease, transport protein) which induces a conformational change in the receptor as illustrated
in the animation above and in the figure link below.
Figure: Models for facilitated diffusion of glucose
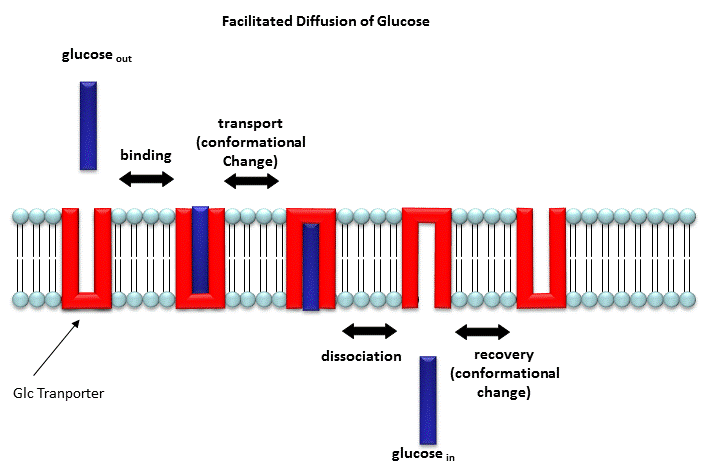
In the latter case, a ligand can bind to the receptor (channel protein) which induces a conformational
change in the receptor, a "ligand-gated" channel through the membrane. This process would lead to the diffusion of many
ions across the membrane (down a concentration gradient) until the channel closes (which can be induced by ligand dissociation
or other events). Clearly, the mathematics we derived for the carrier proteins does not apply to the channel proteins.
In addition, there are other ways to "gate" open a channel protein, which we will discuss later. Also some transporters
can move solute molecules across a membrane against a concentration gradient. These proteins require an external energy
source (like ATP or coupling to the favorable collapse of a second transmembrane gradient ) to drive this thermodynamically
unfavored process. In this section we have discussed only those processes which require no exogenous energy source.
Recently, the x-ray structures of two transporters that are powered by the collapse of a second gradient, were
reported.
Carriers of ligands need not be proteins. Ionophores are small organic molecules
which can bind metal ions and move them down a concentration gradient across a bilayer. Most ionophores are not
resident in the cell membrane. Rather they are mobile carriers of ions. They bind ions in solution, ferry them
through the membrane, and then release them on the other side. As with receptor carrier proteins, they work in both
directions but move ions in a net fashion down the concentration gradient of the ion. One example is valinomycin,
a natural product of Streptomyces fulvissimus,. It is a cyclic peptide consisting of L and D-Val along with L-lactate
and D-hydroxyisovalerate, connected through both ester and amide bonds.
The structure of the valinomycin in its K+ form give clues to its function. The six Val
carbonyl oxygens bind the K+ ion. The hydrophilic groups are pointed toward the center, while the hydrophobic
groups point to the outside of the structure, allowing the K+ ion to be sequesters in a polar environment as the
nonpolar exterior of the complex passes through the membrane. This ionophore is specific for K+ and binds
the smaller Na+ ion weakly. This can be accounted for by two factors. The smaller sodium ion doesn't
bind as tightly to the chelating carbonyl oxygens. Also, the sodium ion has a higher charge density, so the Na+/water
interactions must be more stable and more difficult to break than those to K+. The ion must be desolvated
before it binds to the complex. Other ionophores are specific for other ions.
Some ionophores, like gramicidin, from Bacillus brevis, forms a pore in the membrane through
which different types of Group I ions may flow. It is a 15-residue peptide consisting of alternating D and L amino acids
of significant hydrophobicity. The peptide appears to form a dimer helix (not alpha helix, however), in a bilayer membrane.
(go to the bottom link for next page in the top frame of this page and continue until you get
to the Gramicidin page - an incredible Chime presentation.)
Gram negative bacteria (as well as mitochondria in eukaryotic cells) have protein complexes
called porins. The monomer porin forms a trimer in the membrane which forms a pore allowing small solute molecules
necessary for bacterial cell growth to pass. The porin proteins share a 16 stranded anti-parallel beta barrel as a common
motif. Solute molecules can pass through the pore created by the beta barrel.
Drugs and Diffusion
One of the biggest problems in medical drug development is the productions of drugs that can
diffuse across the cell membrane. This requires that the drug be sufficiently nonpolar while at the same time being
sufficiently polar to have reasonable aqueous solubility, allowing blood transport. One way around this problem is to
develop a water soluble drug and a protein "receptor" which would allow drug passage across the membrane. A novel mechanism
not based on facilitated diffusion has been developed that allows certain protein sequences to transduce the drug across
the membrane (a process called protein transduction or molecular transportation). Researchers have looked to nature
to find proteins which can move across the membrane and adapted them for this process. Several viral proteins
(including TAT from the HIV virus) possess such properties, which derive from the presence of a short sequence in the protein.
Drugs are covalently attached to the sequence, and carried through the membrane by the short protein sequence. This
mechanism does not fit the criteria of facilitated diffusion since the required protein fragment is not a classical receptor.
It is amphiphilic and can pass through the membrane even if synthesized in the lab using D-amino acids or if the sequence
is scrambled. The fusion domain of the TAT protein is ionic (containing 5-15 Arg residues) and probably interacts initially
with negatively charged glycosoaminoglycans on the cell surface. Many different types of drugs can be delivered in this fashion
(large to small, proteins, nucleic acids, and large liposomes, etc). The company Cyclacel is developing a proprietary drug system using another protein transducer, Penetratin, a fragment of the antennapedia protein
from Drosophila.
Another approach is to design artificial receptors. For example, a ligand that might ordinarily bind to
a protein could be covalently modified with a hydrophobic group (often a cholesterol derivative) which would allow it to partition
into the cell membrane, exposing the ligand on the cell surface. The surface ligand can then bind its target protein.
If the protein is multivalent (can bind more than one ligand per protein, such as an antibody), lateral diffusion and clustering
of protein-artificial receptor complexes in the membrane can occur, as well as the formation of lipid rafts. Similar
to other ligand-receptor interactions that display such properties, these membrane changes can lead to endocytosis of the
protein-artificial ligand complex.

