Mb (a monomer containing 8 a-helices, A-H) and Hb (a heterotetramer with two a -and two b-subunits, each which also contains 8 a-helices) are both oxygen binding proteins. Dioxygen is transported from lungs, gills, or skin of an animal to capillaries, where it can be delivered to respiring tissue.  It has a low solubility in blood (0.1 mM).  Whole blood, which contains 150 g Hb/L, and can carry up to 10 mM dioxygen.  Invertebrate can have alternative proteins for oxygen binding, including hemocyanin, which contains Cu and hemerythrin, a non-heme protein.  On binding dioxygen, solutions of Hb change color to bright red.  Solutions of hemocyanin and hemerythrin change to blue and burgundy colored, respectively, on binding dioxygen. Some Antarctic fish don't require Hb since dioxygen is more soluble at low temperature.  Mb is found in the muscle, and serves as a storage protein for oxygen transported by Hb.  Some information about the proteins is given below:

Hemoglobin:

• 1st. protein whose molecular weight was determined
• 1st protein to be assigned a specific function - dioxygen transport
• has a prosthetic group (non-amino acid) heme group (protoporphyrin IX with a ferrous ion) covalently attached which binds dioxygen. 
• 1st protein in which a point mutation (single base pair charge) causes a single amino acid change in the protein, marking the start of molecular medicine
• 1st protein with high resolution x-ray structure
• theory for dioxygen binding explain control of enzyme activity
• the binding of dioxygen is regulated by binding of H+, CO₂, and bisphosphoglcyerate which bind to sites (allosteric) distant from oxygen binding site.
• crystals of deoxy-Hb shatter on binding dioxygen, indicating significant conformational changes on binding.

Heme group:

• The heme group contains protoporphyrin IX,  with four  tetrapyrrole rings linked by methene bridges.  Attached to the tetrapyrrole structure are four methyl, two  vinyl, and two proprionate groups.  These can be arranged in 15 ways, only one (IX) occurs in biological systems.  Ferrous ion bonded to the protoporphyrin IX constitutes the  heme group.
• The heme fits into a hydophobic crevice in the proteins with the proprionate groups exposed to solvent.
• The Fe²⁺  ion is coordinated to 4 N's on the 4 pyrrole rings,  The 5th ligand is a proximal His (the 8th amino acid on helix F).  In the absence of dioxygen, the 6 ligand is missing. and the geometry of the complex is square pyramidal with the Fe above the plane of the heme ring. A distal His (E7) is on the opposite side of the heme ring, but too far to coordinate with the Fe.  When dioxgen binds, it occupies the 6th coordination site and pulls the Fe into the plane of the ring, leading to octahedral geometry.  CO, NO, and H₂S also bind to the 6th site, but with higher affinity than dioxygen, which can lead to CO poisoning.  The distal His keeps these ligands (including dioxygen) bound in a bent, non-optimal geometry.  This minimizes the chances of CO poisoning.
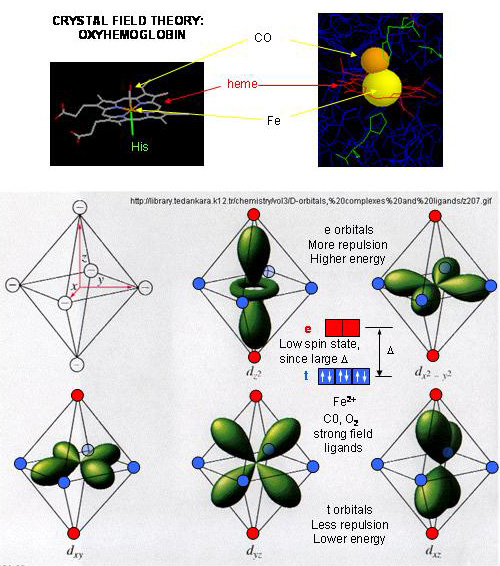
• When oxygen binds to heme Fe²⁺, the geometry of the complex becomes octahedral.  The Fe²⁺ has 6 electrons in d orbitals.  (The electronic configuration of Fe is 3d⁶4s² while the Fe²⁺ ion is 3d⁶).   From crystal field theory (review a general chemistry text), the ligand electrons pairs (treated as anions) interact with the d orbital Fe²⁺ electrons.  They interact most strongly (in a repulsive fashion) with the d_z2 and d_x2-_y2 Fe²⁺ electrons, which are oriented at the axial ends and equatorial corners, respectively, of the octahedral complex.  This repulsion raises the energy of these two orbitals.  The other three d orbitals feel less repulsion by the ligand electrons and are lower in energy.  The difference in energy between the three lower energy levels of d electrons (in t orbitals) and the higher energy levels of electrons (in g orbitals) allows photons matching that energy difference to be absorbed as electrons are promoted to the g orbitals.  Ligands that interact strongly with the d_z2 and d_x2-_y2 electrons raise their energy even more, increasing the energy of the photon required to promote an electron from the t to g orbitals.  Dioxygen is one of those ligands, leading to the absorbance of high energy photons, causing the solution to appear bright red (since blue light is absorbed).  Because of this strong ligand, the significant energy gap between the t and g orbitals causes the electrons to reside mostly in the lower energy t orbitals where they remained paired, giving the complex a low spin state in which all 6 d electrons are paired.  Hence oxyhemoglobin is diagmagnetic.  The heme complex can also exist in a high spin state in which the electrons are easily excited to the g orbitals which are closer in energy to the t orbitals when the ligand is weakly interacting with the Fe²⁺ electrons.  In these cases, the heme is paramagnetic since unpaired electrons are possible.  (We will discuss paramagnetism latter in the course during our exploration of oxygen chemistry.  

Figure:  Heme-O₂ Octahedral Complex

• When dioxyen binds, the oxidation state of the  Fe²⁺   ion does not change, even through dioxygen is a great oxidizing agent.  Hence the  Fe²⁺  ion is a reversible carrier of dioxygen not of electrons.   Free heme in solution is oxidized by dioxygen, forming a complex with water which occupies the 6th position, with  the iron in the  Fe³⁺  state.   An intermediate in this process is the formation of a dimer of 2 hemes linked by 1 dioxygen.  This can't occur readily when the heme is in Hb or Mb.   Other heme proteins (like Cytochrome C) are designed to be carriers of electrons.
• A small amount of the  Fe²⁺  ion gets oxidized to  Fe³⁺  ion.  Mb and Hb in this state are called metHb and metMb.  A enzyme is required to reduced the iron back to the  Fe²⁺  state. 

Myoglobin

• Mb is extremely compact, and consists of 75% alpha helical structure.
• 8 a-helices are present, labeled A-H. 
• 4 alpha helices are terminated by Pro
• The interior amino acids are almost entirely nonpolar.  The only polar amino acids found completely buried are the two His (proximal and distal) found at the active site of dioxygen binding.

Difference between Hb and Mb

• Hb is a tetramer of two a and two b subunits held together by IMF's (an example of quarternary protein structure), and 4 bound hemes, each of which can bind a dioxygen.   In a fetus, two other subunits make up Hb (two zeta - z and two epsilion - e subunits -analogous to the two a and two b subunits, respectively).  This changes in fetuses to two a  and two  g subunits. Fetal Hb has higher affinity for dioxygen than adult Hb.  Mb is a single polypeptide chains which has higher affinity for dioxygen than Hb.
  
  The  a and two b chains are similar to Mb, which is unexpected since only 24 of 141 residues in the a and b chains of Hb are identical to amino acids in Mb.  This suggests that different sequences can fold to similar structures.  The globin fold of Mb and each chain of Hb is common to vertebrates and must be nature's design for dioxygen carriers.  A comparison of the sequence of Hb from 60 species show much variability of amino acids, with only 9 identical amino founds.  These must be important for structure/function.  All internal changes are conservative (e.g. changing a nonpolar for a nonpolar amino acid).  Not even Pro's are conserved, suggesting there are different ways to break helices.  The two active site His are conserved, as is Gly B6 (required for a reverse turn).

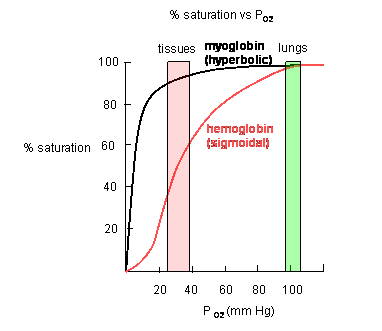
• Plots of Y (fractional saturation) vs L (pO₂) are hyperbolic for Mb, but sigmoidal for Hb, suggesting cooperative binding of oxygen to Hb (binding of the first oxygen facilitates binding of second, etc). (see Preclass Question Below.)

Figure:  Plots of Y (fractional saturation) vs L (pO₂) are hyperbolic for Mb, but sigmoidal for Hb

• The affinity of Hb, but not of Mb, for dioxygen depends on pH.   This is called the Bohr effect, after the father of Neils Bohr, who discovered it.

Figure:  Bohr effect

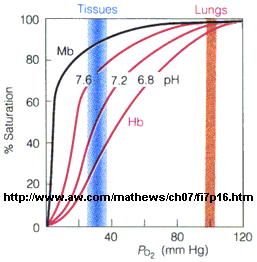
• Protons (decreasing pH), carbon dioxide, and bisphosphoglycerate, all allosteric ligands which bind distal to the oxygen binding sites on the heme, shift the binding curves of Hb for oxygen to the right, lowering the apparent affinity of Hb for oxygen. The same effects do not occur for Mb. These ligands regulate the binding of dioxygen to Hb.

From these clues we wish to understand the molecular and mathematical bases for the sigmoidal binding curves, and binding that can be so exquisitely regulated by allosteric ligands. The two obvious features that differ between Mb and Hb are the tetrameric nature of Hb and its multiple (4) binding sites for oxygen.  Regulation of dioxygen binding is associated with conformational changes in Hb.

MOLECULAR BASES FOR CONFORMATIONAL CHANGES

Based on crystallographic structures, two main conformational states appear to exists for Hb, the deoxy (or T - taut) state, and the oxy (or R -relaxed) state. The major shift in conformation occurs at the alpha-beta interface, where contacts with helices C and G and the FG corner are shifted on oxygenation.

Figure: alpha-beta interface

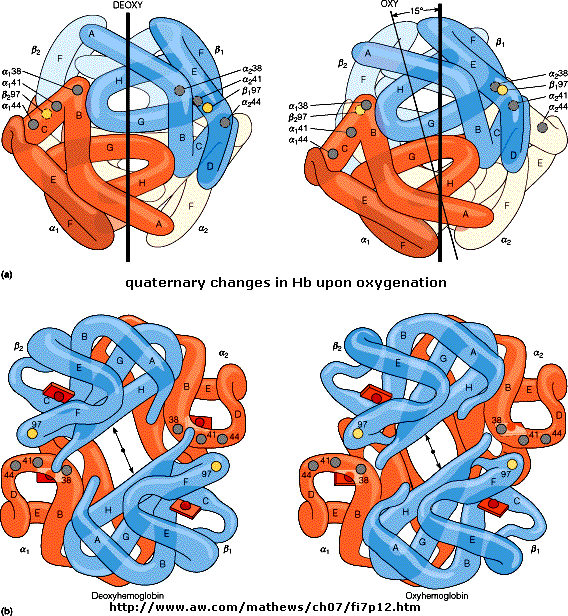
The deoxy or T form is stablized by 8 salt bridges which are broken in the transition to the oxy or R state.

Figure:  8 salt bridges

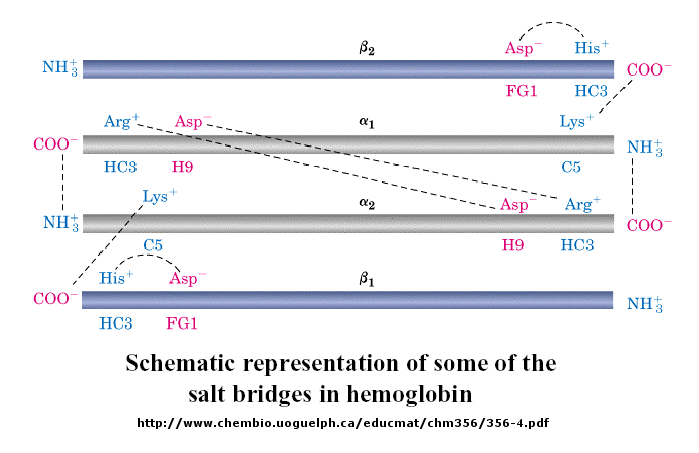
6 of the salt bridges are between different subunits (as expected from the above analysis), with 4 of those involving the C- or N- terminus.

Figure:  C- or N- terminus

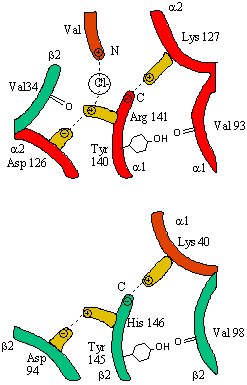
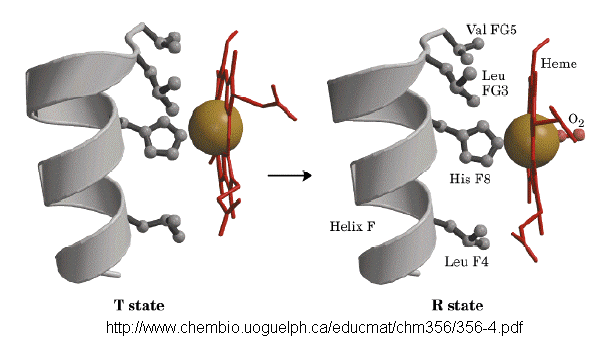
 In addition, crucial H-bonds between Tyr 140 (alpha chain) or 145 (on the beta chain) and the carbonyl O of Val 93 (alpha chain) or 98 (beta chain) are broken. Crystal structures of oxy and deoxy Hb show that the major conformational shift occurs at the interface between the a and b subunits. When the heme Fe binds oxygen it is pulled into the plan of the heme ring, a shift of about 0.2 nm. This small shift leads to larger conformational changes since the subunits are packed so tightly that compensatory changes in their arrangement must occur. The proximal His (coordinated to the Fe) is pulled toward the heme, which causes the F helix to shift, causing a change in the FG corner (the sequence separating the F and G helices) at the alpha-beta interface as well as the C and G helices at the interface, which all slide past each other to the oxy-or R conformation.

Figure:  F helix to shift

THE MOLECULAR BASES FOR ALLOSTERIC EFFECTS:

Decreasing pH shifts the oxygen binding curves to the right (to decreased oxygen affinity). Increased [proton] will cause protonation of basic side chains. In the pH range for the Bohr effect, the mostly likely side chain to get protonated is His (pKa around 6), which then becomes charged. The mostly likely candidate for protonation is His 146 (on the b chain - HC3) which can then form a salt bridge with Asp 94 of the b (FG1) chain.  This salt bridge stabilizes the positive charge on the His and raises its pKa compared to the oxyHb state.  Carbon dioxide binds covalently to the N terminus to form a negatively charge carbamate which forms a salt bridge with Arg 141 on the alpha chain. BPG, a strongly negatively charged ligand, binds in a pocket lined with Lys 82, His 2, and His 143 (all on the beta chain).    It  fits into a cavity present between the b subunits of the Hb tetramer in the T state.   Notice all these allosteric effectors lead to the formation of more salt bridges which stabilize the T or deoxy state. The central cavity where BPG binds between the b subunits become much smaller on oxygen binding and the shift to the oxy or R state.  Hence BPG is extruded from the cavity. 

The binding of H⁺ and CO₂ helps shift the equilibrium to deoxyHb  which faciliates dumping of oxygen to the tissue.  It is in respiring tissues that CO₂ and H⁺ levels are high.  CO₂ is produced from the oxidation of glucose through glycolysis and the Krebs cycle.  In addition, high levels of CO₂ increase H⁺ levels through the following equilibrium:

H₂O  +  CO₂  <==>  H₂C0₃   <==>  H⁺  +  HCO₃-

In addition, H⁺ increases due to production of weak acids such as pyruvic acid in glycolysis . 

Hb, by binding CO₂ and H⁺, in addition to O₂, serves an additional function:  it removes excess CO₂ and H⁺ from the tissues where they build up.  When deoxyHb with bound H⁺ and CO₂ reaches the lungs, they leave as O₂ builds and deoxyHb is converted to oxyHb.

MATHEMATIC BASES FOR THE SIGMOIDAL BINDING CURVE FOR OXYGEN.

Previously we have shown that the binding of oxygen to Mb, which can be described by the equilibrium,

M + L <=> ML, can be described mathematically by

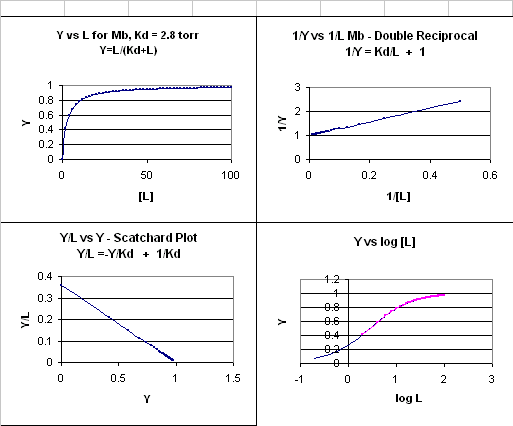
1)  Y = L/[Kd +L].

This is the equation of a hyperbola. Remember, that this hyperbolic plot can be transformed in a variety of ways, as summarized in the graphs below for Mb.

Figure:  4 Ways to plot Mb and O2 plots  

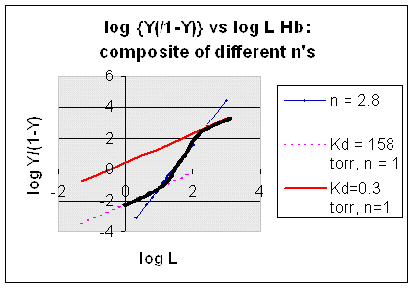
How does the sigmoidal binding curve for Hb arise. At least three  models (Hill, MWC, and KNF) can be developed that give rise to sigmoidal binding curves. Remember, sigmoidal curves imply cooperative binding of oxygen to Hb: As oxygen binds, the next oxygen seems to bind with higher affinity (lower Kd)

Hill Model: In this model, we base our mathematical analysis on the fact that the stoichiometry of binding is not one to one, but rather 4 to 1: Perhaps a more useful equation to express the equilibrium would be M + 4L <=> ML₄. For this equilibrium, we can derive an equation analogous to the equation 1 above. This equation is:
2)   Y = L⁴/[Kd + L⁴].

For any given L and Kd, a corresponding Y can be calculated. Using this equation, the plot of Y vs L is not hyperbolic but sigmoidal (see next link below).  Hence we're getting closer to modeling that actual data.  However, there is one problem.  The sigmoidal curves doesn't give a great fit to the actual oxygen binding curve for Hb.   Maybe a better fit can be achieved by altering the exponents in equation 2. A more general equation for binding might be M + nL <=> ML_n, which gives the following equation:

3)   Y = Lⁿ/[Kd + Lⁿ].

If n is set to 2.8, the theoretical curve of Y vs L gives the best but still not perfect fit to the experimental data.  It must seem arbitrary to change the exponent which seems to reflect the stoichiometry of binding. Consider another meaning of the equilbrium described above:
M + 4L <=> ML₄. One interpretation of this is that all 4 oxygens bind at once to Hb. Or, alternatively, the first one binds with some low affinity, which through associated conformational changes changes the remaining 3 sites to very high affinity sites which immediately bind oxygen if the oxygen concentration is high enough. This model implies what is described as infinitely cooperative binding of oxygen.

(Notice that this equation becomes: Y = L/[Kd + L], when n =1 (as in the case with myoglobin, and in any equilbrium expression of the form:  M  +   L  <==>  ML.  Remember plots of ML vs L or Y vs L gives hyperbolas, with Kd = L at Y = 0.5.)

Does Kd = L at Y = 0.5?    The oxygen concentration at which Y = 0.5 is defined as P₅₀. We can substitute this value into equation 3 which gives an operational definition of Kd in terms of P₅₀.
Y = 0.5 = P₅₀ⁿ/[Kd + P₅₀ⁿ] - multiple both sides by 2
1 = 2P₅₀ⁿ/[Kd + P₅₀ⁿ]
Kd + P₅₀ⁿ = 2P₅₀ⁿ
4)  Kd = P₅₀ⁿ
Note that for equation 3,  Kd is not the ligand concentration at half-saturation as we saw in the case with hyperbolic binding curves.

Now consider another model:

M + L <=> ML + L <=> ML₂ + L <=> ML₃ + L <=> ML₄ where the binding of each oxygen to the unligated or increasing ligated Hb has the same Kd. That is, the affinity of each binding site for oxygen does not increase as more sites are bound to oxygen. In this model, n in equation 3 is 1, and the resulting graph is completely hyperbolic. The fact that the experimental data fits the equilbrium M + 2.8L <=> ML_2.8 implies that the binding is cooperative but not infinitely cooperative.  Graphs of Y vs L showing these three cases (n=1, 2.8, and 4) are shown below:

Figure:  Plots of Y vs L for Hb with varying degrees of cooperativity:  n = 1, 2. 8, and 4

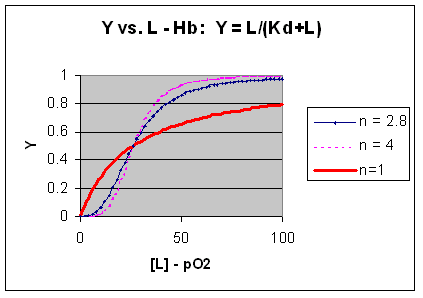
The general equation 3),  Y = Lⁿ/[Kd + Lⁿ] can be rearranged as shown below:
 
1 - Y = [Kd + Lⁿ]/[Kd + Lⁿ] - Lⁿ/[Kd + Lⁿ] =
 
5)   1 - Y = Kd/[Kd+ Lⁿ]
 
where 1 - Y is the fraction not bound. Solving for Y/[1-Y] by using equations  3 and 5 gives:
 
6)   Y/[1-Y] = {Lⁿ/[Kd + Lⁿ]}/ Kd/[Kd + Lⁿ] = Lⁿ/Kd.

Taking the log of both sides gives:
 
log (Y/1-Y) = log ( Lⁿ/Kd) =
 
7)   log (Y/1-Y) = nlog L - log Kd
 
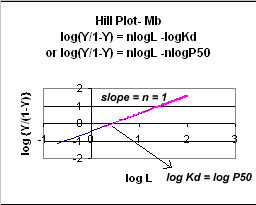
A plot of log (Y/1-Y) vs log L is called a Hill plot, where n is the Hill coefficient.   This equation is of the form: 
y = mx + b which is a straight line with slope n and y intercept of - log Kd.  When n = 1, as it would be with Mb or Hb when oxygen binds to each site with the same affinity irrespective of the number of other oxygens bound to other sites, the Hill plot is linear with a slope of 1. Solving for the x intercept (when the y axis variable is 0) in equations 7 gives:
 
8)   0 = nlog L -log Kd, or nlogL = log Kd, or log L = (logKd)/n.

The X intercept is when the dependent variable "y" value is 0. This occurs when Y/(1-Y) = 1, which occurs  at half fractional saturation. (Remember log 1 = log 10⁰ = 0)

Substituting equation 4  (Kd = P₅₀ⁿ) into (7) and (8) gives
(9) log (Y/1-Y) = nlog L - n log P₅₀ - the Hill Equation with P₅₀ instead of Kd,
(10) 0 = nlog L -nlog P₅₀, or nlogL = nlog P₅₀, or log L = logP₅₀.

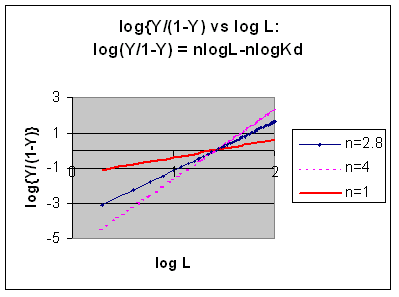
Even when n does not equal 1, the Hill plot is linear, since it has the form y=mx+b.  If n = 2.8 or 4, the plot is linear, but has a slope of 2.8 and 4, respectively.    This can be seen in the graph below which shows HIll plots with n = 1, 2.8, and 4.

Figure:  Hill Plot for Mb (n =1)

Hill Plots:  n = 1, 2.8, and 4

However, the affinity of dixoygen for Hb changes, so that there must be more than one effective Kd.  Hence, the actual Hill  plot of Hb,  log (Y/1-Y) vs log L, can not be linear over all ranges of dioxygen.   A linear plot, such as for Mb, crosses the x axis at one point, with a value of (logKd)/n = logKd since n = 1.  In contrast for Hb, since the Kd seems to change with L concentration, there can not be just 1 value of Kd, as given by the x intercept.  The Hill plot of actual Hb binding data is curvilinear, and cross the x axis only once.  Howver, the ends of the curve (at low and high dioxygen) approach straight lines with slopes of 1 (i.e. n=1).  If extrapolated through the x axis, these lines would give the Kd for the binding of the first and last dioxygens, which bind noncooperatvely.  LogL values near the region of the curve that crosses the x axis approximate a straight line with slope of  2.8.   This implies there is maximal cooperativity in the middle of the binding curve.  The graphs shows that the Kd for the first oxygen binding is much higher than the Kd for the last oxygen binding. Hence the Hill Plots supports our ideas than cooperativity is caused by conformational changes in Hb which occur on oxygen binding such that as progressively more oxygen is bound, the affinity for the remaining sites increases.

Figure:  Hill Plots For Hb Showing straight lines for n=2.8 and for n's=1 which model the low and high affinity sites.

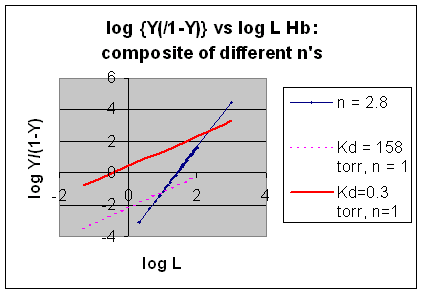
Figurre:  Hill Plot for Hb:  Black line showing hypothetical actual curve

MWC (Monod, Wyman, and Changeux)- Symetry Model: In this model, in the absence of ligand (oxygen), Hb exists in two distinct conformations, the T state (equivalent to the crystal structure of deoxyHb) and the R state (equivalent to the crystal structure of oxyHb without the oxygen). In the absence of dioxygen, the T state (T₀) is greatly favored over the unliganded R state  (R₀) at equilibrium. An equilibrium constant (more equivalent to a dissociation constant) can be defined as L = T₀/ R₀.  (Note:  L is not the ligand concentration.)  In addition, let us assume that Hb can not exist with some of the monomer in a tetramer in the T state while others in the same tetramer are in the R state. Hence this model is often called the symmetry model. Finally lets assume that each oxygen can bind to either the T or R state with the dissociation constants K_T and K_R respectively. These constants do not depend on the number of oxygens already bound to the tetramer. Hence K_R = [R₀][O₂]/[R₁] = [R₁][O₂]/[R₂] = ... etc., where the subscript on R refers to the number of oxygens bound to that form of R.

Figure:   LINKED EQUIIBRIA IN THE MWC MODEL

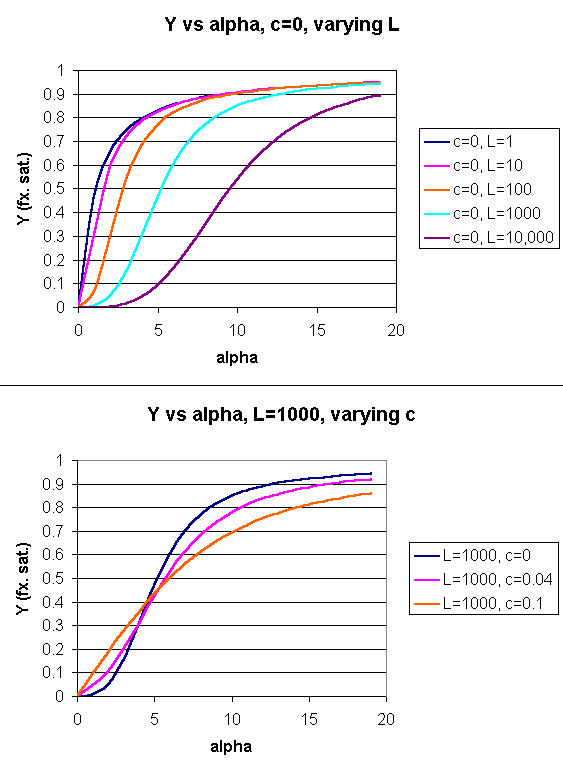
Now define two new parameters:
a = [pO₂]/K_R which is really a normalized ligand concentration describing how many times the K_R the ligand concentration is.

c = K_R/K_T.

If oxygen binds preferentially to the R form of Hb, c would be a small fractional number. In the limiting case, when oxygen didn't bind to the T form, K_T would be infinite, and c would equal 0.

Using these definitions and equations, the following equation showing Y, fractional saturation vs a can be derived, with n, the number of binding sites per molecule, = 4 for Hb.

Y = [a (1+a)^n-1 + Lca(1+ca)^n-1]/[(1+a)ⁿ +L(1+ca)ⁿ]

 Figure:  Y Vs alpha with varying L and c - MWC MODEL

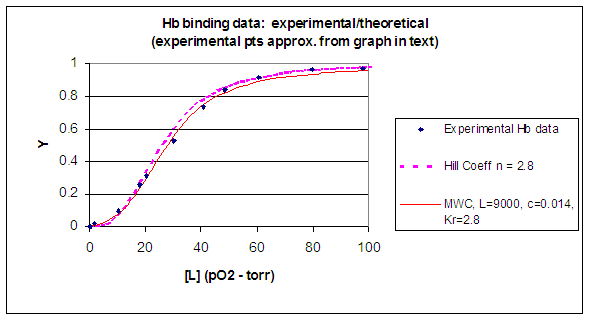
When L is set at 9000 and c = 0.014, the Y vs a curve fits the experimental oxygen binding data well. The graph below shows the best experimental dioxygen binding data that I could find (obtained from a graph, not from a table), and the best fit Y vs L using a Hill coefficient of n=2.8 (fitting equation 3 above), and the best fit of Y vs L using the MWC model, with L=9000, c=0.014, and Kr = 2.8 torr. 

Figure:  Hb binding curves:  Experimental, vs Theoretical Hill and MWC Equations

Mathcad 8 - MWC Model for Oxygen binding to Hb

Another way to think about the MWC Model

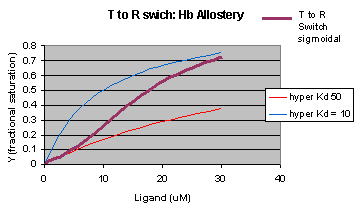
The MWC model assumes that oxygen binds to either the T or R form of Hb in a noncooperative fashion. That is K_T and K_R are constant, independent of the number of oxygens bound to that form.  If that is so, what is the basis of the cooperative oxygen binding curves?  The answer can be seen below.  The red curve might reflect the binding of a ligand to the T form of a macromolecule, with Kd = 50 uM, for example.  Notice that the binding curve is hyperbolic.  Likewise, the blue curve might reflect the binding of a ligand to the R form of the macromolecule with Kd = 10 uM.  If the T and R form are linked through the T <==> R equilibrium, this equilibrium will be shifted to the tighter binding R form with increasing ligand concentration, assuming that the ligand binds preferentially to the R form.  This shifts the actual binding curve from that resembling the T form at low ligand (red) to that of the R form as ligand increases (blue), imparting sigmoidal characteristics to the actual binding curve (purple).

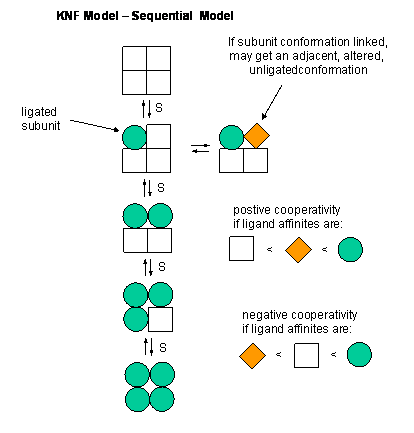
KNF (Koshland, Nemethy, and Filmer) - Sequential Model: This model was developed to address concerns with the concerted model. One of the major problems with the concerted model is that it seemed unrealistic to expect all the subunits to change conformation together. Why shouldn't there be some difference in subunit conformation? The KNF model also fits the experimental data well. 

Figure:  EQUILIBRIA IN KNF MODEL

Web Links:

• A Review of Hb Allostery from Mathews, van Holde, and Ahern.  
• Figure showing MWC and KNF Models  from Mathews, van Holde, and Ahern

LINKED EQUILIBRIA

Hemoglobin is an amazing molecule. Unlike myoglobin, in displays cooperative binding of dioxygen. In addition, not only does it bind dioxygen (at the heme Fe), it also binds protons and carbon dioxide at other, or allosteric sites. Binding of these ligands influences the binding of dioxygen, as seen from the right ward shift of the oxygen binding curves at lower pH's, such as would be encountered in respiring tissues. The linkage of the binding of dioxygen, and protons or carbon dioxide can be visualized easily with simple thermodynamics which you learned in general chemistry. Consider the equilibria shown below.

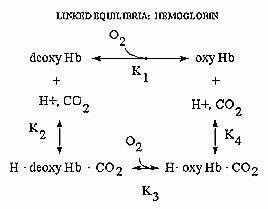
It should be obvious from these equations than K₁ K₄ = K₂ K₃ , where K_i are the dissociation constants for the various equilibrium. Remember than DG is a state function and independent of path. Hence DG^o₁ + DG^o₄ = DG^o₂ + DG^o₃ , where DG^o_i = -RTln(1/Kd_i). From the oxygen binding graphs, it is also clear that K₁ < K₃. Therefore, it is clear that K₂ < K₄. This shows that protons binds to deoxyHb more tightly than to oxyHb. Hence, the presence of higher [H⁺] drives the dissociation of O₂ from oxyHb. As described in the book, H⁺ bind to side chains which have an increased affinities for H+ in the deoxyHb state. The conformation change in Hb alters the effective environment of some side chains (specifically His b146, His a122, and the a amino group of the a chain), increasing their pKa values The protonated HisH⁺ then makes a salt bridge to Asp b 94 in the FG corner of the same b chain, forming a salt link which stabilizes the deoxyHb or taut state.

Figure:  A review of thermodynamic cycles - linked equilibria - other examples

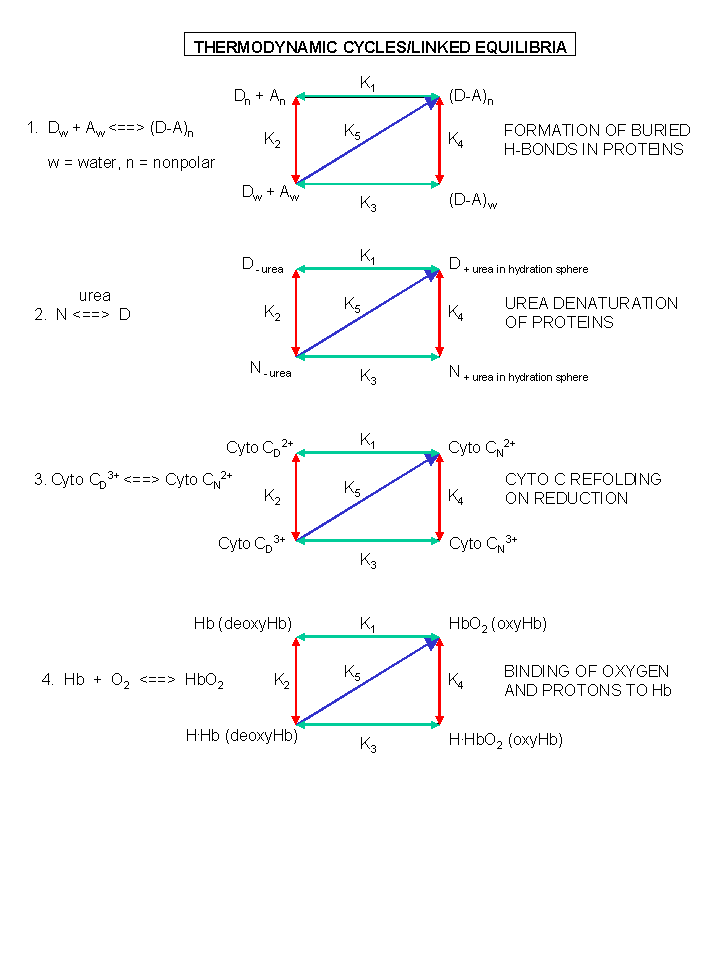
Other Examples of Conformational Changes in Biological Macromolecules

Conformational changes in macromolecule structure upon ligand binding are common features of such interactions.  Interesting examples of conformational  effects on binding are described below.   Protein activities can often be modeled using the assumption of two major, different conformational forms.  The first example, however, describes time-resolved  structural changes in a protein on ligand release.

Unbinding of a ligand from a protein

As a complete understanding of an organic reaction requires a knowledge of the structures of reactants, transition states, intermediates and products along the reaction coordinates, so is the knowledge of different structural states along the dissociative pathway necessary for a complete understanding of the dissociative (and by inference the associative) mechanisms of ligand binding.  Such a time-resolved pathway can be studied through molecular dynamics simulations.  Schotte et al. have recently studied the dissociation of CO from carboxy-L29F-myoglobin to deoxy-L29F-Mb using time-resolved x-ray crystallograhy.  (L29F is a mutant form of the wild type in which Leu 29 has been changed to Phe.)  They chose this mutant since evidence of a short-lived (140 ps lifetime) intermediate in the flash-photolyzed dissociation of CO from the mutant was found using time-resolved mid-infrared spectroscopy of CO-L29F-myoglobin.  In this technique, the CO-L29F-Mb is pulsed with an orange laser to photolyse the CO-Mb complex. After a brief delay, an IR pulse tuned to the CO stretch was added.  The spectra of the mutant Mb showed two bands which converted to one broad band with time.  The two bands represent two different orientations of the CO at the heme Fe, while the broad band arises when the CO dissociates from the primary site to other sites.  The intermediate represented a structure in which CO was trapped in a binding site adjacent to the heme Fe which presumably is also a binding site for the initial association of the ligand.  This site found in molecular dynamics simulations consisted of the heme and Val68, Ile 107, and Leu29 side chains, all of which are conserved in mammalian myoglobins.  Time-resolved x-ray structures were obtained after orange laser-induced photolysis, followed by time-delayed x-ray pulses.  These structures showed much larger changes in structure than the differences in structure between the deoxy-and oxy-Mb x-ray structures would suggest.  The side changes exhibits coordinated motions that "sweeps" the CO away, accounting for the fast dissociation of the bound CO.

An Engineered Allosteric Enzyme

Do you ever wonder if your respiratory infection is viral, bacterial, or fungal in origin?  Most patients would probably like an antibiotic but with the rise of resistant bacteria, unwarranted use of antibiotics is not wise.  Wouldn't it be great if a quick test could be done to distinguish among these possibilities?  A new sensitive and rapid method to analyze for specific DNA sequences (which could provide the needed distinction) has been developed by Saghatelian et. al.  They have made an enzyme with a covalently attached single-stranded DNA sequence - an inhibitor-DNA-enzyme (IDE) complex. 

Figure:  inhibitor-DNA-enzyme (IDE) complex

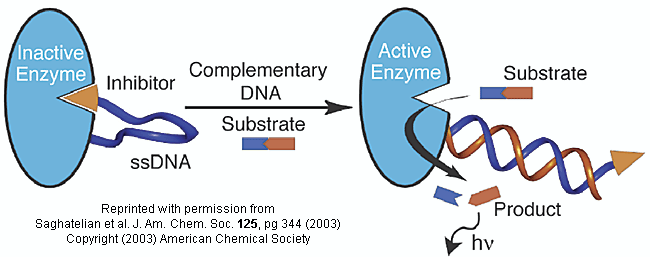
To the other end of the DNA is covalently attached an inhibitor of the enzyme.  The inhibitor, tethered to the ssDNA, can bind to and inhibit the enzyme.  Now if a complementary strand of DNA (derived from the bacterial, virus, etc) is added, it can bind to the ssDNA tether through complementary H-bond interactions to form a dsDNA in which the inhibitor is removed from the active site of the enzyme.  The complementary DNA is, in effect, an allosteric activator, or more accurately a deinhibitor, of the enzyme.  If a substrate is now added which can bind to the enzyme active site and form a  fluorescent product, a very sensitive and quick assay is available.  Saghatelian used a protease from B. cereus (CNP) and the substrate DABCYL-peptide-EDANS.  The DABCYL group on this substrate is a quencher or the EDANS fluorophore.  When cleaved by the enzyme, EDANS fluoresces intensely. The assay detected 10 fmol of DNA in less than three minutes. 

Circadian Rhythms and the Biological Clock

Many human behaviors are cyclic with a repeat period of 24 hours (such as sleep/wake cycles).  These circadian rhythms, which can be phase-shifted by alternations in environmental cues (such as light intensity, sleep deprivation) must have some biochemical basis.  Understanding the mechanisms underlying circadian rhythms and its regulations would prove helpful in developing new ways to help people minimize the influence of jet lag or shift work.  In humans, light intensity information is transmitted from the retina to the suprachiasmatic nucleus in the hypothalmus (in the brain), which then signals the pineal gland (behind the hypothalmus) to secrete the hormone melatonin.  Its levels rise at night and fall in the day, but its biochemical mechanism of action is still being determined.  Other hormones are also involved.  What are the biochemical targets of these hormones?  What is the basis of circadian changes in individual cells?

One such protein is the membrane enzyme (Hydroquinone) NADH Oxidase (NOX).  NADH is a small cellular reducing agent that we will discuss in the future.  This enzyme is found in the external plasma membrane of all human cells, including tumor cells.  NOX proteins are very usual in that they possess two activities:  a NADH oxidase activity (measured by the disappearance of of NADH) and a protein disulfide isomerase (thiol interchange) activity (measured by the renaturation of RNase A using cCMP as a substrate or the cleavage of dithiodipyridine).  These activities alternate in a temporal sense with a 24 minute period!  The normal cellular form of the protein is constitutively expressed and responsive to hormones.  A form found specifically on tumor cells, tNOX, is inhibited by certain  chemotherapeutic drugs and by capsaicin (the active ingredient in hot peppers), and is not responsive to hormones (suggesting unregulated activity).  tNOX has a 22 minute period.  In cancer patients, a truncated form of tNOX (ttNOX), formed by limited proteolysis from tNOX, is found in the serum.  NOX proteins are also resistant to proteases and can self aggregate to form "amyloid" type fibrils similar to those found in prion diseases.  They can also interact with other proteins and render them protease resistant.  The temporal periods of both proteins are independent of temperature and can be "entrained" through the appropriate stimuli.  What structural features of the protein can account for unique properties.  Early evidence (using FTIR and CD) suggests that changes in secondary structure (similar to prion proteins) occurs involving changes from alpha helices to beta sheets.  Perhaps the protein can exist in two distinct, yet similar conformations, each with a different activity.

The tNOX gene has been cloned and expressed.  It encodes a protein of 610 amino acids, and its activities, when expressed in bacteria, cycle in 22 minutes.  Site-specific mutations produce periods of 36 minutes (for Cys575Ala) and 42 minutes (for  Cys558Ala) mutants.  These proteins show the same activities and periods when produced in transformed eukaryotic COS-1 cells.  This cell surface proteins affects the circadian rhythms of the whole cell.  A normal protein in the cell, glyceraldehyde -3-phosphate dehydrogenase, (GAPDH) exhibits a 24 hour activity circadian rhythm in normal COS cells (which have a constitutively expressed NOX gene product).  When transformed with the mutants, the demonstrate not only a 24 hour GAPDH activity, but in addition, a 22, 36, or 42 hour activity when transformed with the gene for tNOX, the tNOX Cys575Ala mutant,  and the tNOX Cys558Ala mutant respectively. 

HIV Binding to T helper immune cells

It has been notoriously difficult to develop a vaccine against the HIV virus.  One type of vaccine results in the formation of protective proteins called antibodies, which bind to an immunogen in the vaccine and ultimately to a "foreign" molecule such as a protein on the surface of an actual virus or bacterial cell.  The HIV has a surface protein, gp120, which binds to a receptor protein, CD4, on the surface of certain immune cells like the T helper cell.  If this interaction could be prevented, then HIV could not enter cells.  Many attempts have been made to develop neutralizing antibodies to gp120  by using gp120 and variants as an immunogen.  These have all failed.  Further work has shown that when gp120 binds to the receptor protein CD4, the gp120 undergoes a conformational change which allows a newly exposed loop on gp120 to bind to yet another coreceptor, CCR5, on the immune cell, facilitating virus uptake into the cell.  The exposed loop conformation of the gp120 seems to resemble the structure of a normal protein ligand (the chemokine RANTES) for the CCR5 receptor.  Such examples of molecular mimicry are becoming more common. Recently, the crystal structure of an unliganded simian virus gp120 protein has been determined (Chen et al.).  Comparison of this to the bound form (to CD4) shows clear conformational changes.  Small inhibitors could be designed to the unbound form, locking it in that conforrmation which would prevent viral entry into cells.

Isomeric Antibodies

In our study of hemoglobin structure in the MWC model, we developed the idea that there were two forms of hemoglobin in solution, the taut and relaxed form, which are pre-exisiting and interconvertible even in the absence of dioxygen.  Oxygen was presumed to bind preferentially to the relaxed form.  In the KNF model we saw that ligand binding can induce conformational changes in adjacent subunits, promoting cooperative binding of ligand.  In general these two models distill down to combinations of two simpler models.  The first might be called the lock and key model in which ligand binds tightly to a preexisting conformations without inducing subsequent macromolecular conformational change. Alternatively, the ligand might bind loosely and then alter the macromolecular conformation to produce tighter binding, an example of an induced fit model.   For the binding of dioxygen to hemoglobin, thermodynamic cycles could be drawn showing either binding of ligand and subsequent conformational changes in protein structure or conformational changes in protein structure proceeding binding.  Is there additional evidence to support the lock and key binding of ligand to a protein that can, in the absence of ligand, exist in two conformations?  The answer is yes.

Antibodies are immune system protein molecules than can bind "foreign" molecules and target them biological neutralization.  Many crystal structure have been determined of antibodies in the presence or absence of a "foreign" ligand molecule.  In these cases, the conformation of the bound antibody is different from that of the free.  Either an and induced fit model for ligand binding or a lock and key model of binding of ligand to one of two different pre-existing conformations of the antibody could account for this observation. These different mechanisms could be differentiated experimentally by stop-flow kinetic technique since both display slow and fast phases that are affected differently by ligand concentration.  Theoretically, in the induced fit model, only one ligand type could bind to the antibody which would undergo a conformational rearrangement to produce tighter binding. However, in the two preexisting conformational model, a different structural ligand might bind to each of the two main antibody conformations.  James et al. have recently shown through stop flow kinetics techniques (to investigate binding) and x-ray crystallography (to investigate final structures) that one antibody molecule can, through existing in two different preexisting conformations, bind two different ligands (antigens).  One antibody conformations binds small aromatic molecules with low affinity (including the small molecule 2,4-dinitrophenol, the immunizing molecule or hapten) and then rearranges to produce a high affinity binding complex in which the DNP is bound in a narrow cavity (reducing the effective off rate of the bound ligand.  A second antibody conformation  binds a protein ligand over a broad, flat binding site of the antibody molecule. 

FREE ENERGY AND COOPERATIVITY

Please Note:  I probably won't cover this section in class given time constraints.  It is a great example of the use of thermodynamic cycles in modern biochemical analysis.  Consider it optional material at this point in time. 

To change the conformation of deoxyHb to oxyHb requires energy (about 6 kcal/mol, or the equivalent of about 2 H-bonds. Remember from our discussion of protein stability, proteins are not inherently all that stable. They denature at modest temperatures, and are stabilized over the native state only about 10 kcal/mol for a typical protein of 100 amino acids. Energy changes in proteins can arise from ligand binding, or tertiary/quaternary structural changes in the protein. Consider the following important points about O₂ binding.

• the beta chain of Hb binds O₂ noncooperatively, with a Kd similar to Mb.
• the hemoglobin tetramer (T) readily dissociates into alpha-beta dimers (D), which also bind O₂ with high affinity, and noncooperatively.

Hence, when 2D ----> T, there is an energy penalty in the form of a greatly reduced O₂ affinity, but what is acquired is the property of cooperativity for O₂ binding, which facilitates maximal unloading of O₂ under physiological conditions. This cooperativity can be measure as DG_coop = DG_c, where
DG_c = DG_{O2 bind to tetramer} - DG_{O2 bind to same site on dimer, or}
DG_c = DG_T - DG_D. The DG_T and the DG_D can be determined from the binding isotherms (Y vs [O₂] at various dilutions of the tetramer). Then DG_c can be calculated. The results are shown below.

Table 1: Free Energy of Oxygen Binding to Hb T and D.

The tables above show the DG_c for oxygen binding to various states of Hb. Notice that DG_c is positive for the first 3 bindings, and negative for the last.

The cooperativity models for oxygen-Hb binding (the MWC -concerted model and the KNF- sequential model) are based on the two end states (fully ligated and fully unligated) and the stepwise states (1, 2, or 3 O₂ bound). They do not describe binding to specific sites on the Hb tetramer. That is, they do not reflect the different possible microstates. For example, there are 4 different microstates possible in which 2 O₂ are bound to the tetramer (see Table 1). There are 8 different possible partially liganded microstates (Table 1). It has been difficult to study each of these microstates directly since it is impossible to isolate them in pure form, or to resolve their different properties in a mixture. Three reasons account for this:

• each state is labile and O₂ exchanges among the states
• the tetramer (T) dissociates to 2D which reassociates to give hybrids.
• the lower relative abundance of intermediates in a cooperative system.

This problem was solved by suing CO, NO, and CN as ligands, since they bind more tightly. Also the Fe can be replaced with Co(II) or Mn (III). We have studied linked equilibrium before:

• 2 N-methylacetamide monomers (aq) ---> N-methylacetamide H-bonded dimer (nonpolar)
• deoxyHb <---> oxyHb in the presence of H+ and CO₂ (see above)

We have seen, especially in the former case how thermodynamic cycles or linked equilibria can be used to calculate DG and K's for reactions which would be difficult to carry out. Let us now apply these concepts to Hb binding to ligands. Specifically, we wish to calculate DG_c from the D Gs for binding of a ligand to a specific site on a dimer and on the tetramer, as shown below.

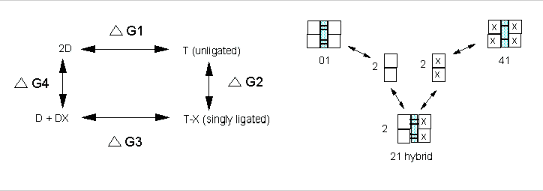
It should be obvious that:

DG^o₁ + DG^o₂ = DG^o₃ + DG^o₄ , or DG^o₃ - DG^o₁ = DG^o₂ - DG^o₄ = DG^o_c . It is not difficult to determine DG^o₃ - DG^o₁ which can be determined using gel filtration chromatography since dimers can readily be separated from tetramers. Methods can be developed to prepare individual microstates and then the assembly free energy can be determined. From this, using thermodynamic cycles, the DG^o_c can be calculated. The results for a Cyanomet Hb microstates are shown in Table 2. The 10 microstates are distributed into 3 distinct cooperative free energies. This suggests that there may be a problem with the MWC model which proposes 2 quaternary states, the T and the R. Is there a third quaternary state, or is there a change in the tertiary structure of the R or T states which generate 3 kcal/mol of cooperative free energy? If the unligated "deoxy"state is the T state, and if the microstates 11,12, and 21 are also assigned to the T state, then the T -->R transition occurs when binding creates a tetramer with 1 or more ligated subunits on each side of the dimer/dimer interface.

The overall DG_c is generated by two different conformational changes. On binding the first ligand, global conformational changes occur in the ligated dimeric state. The D/D interface acts as a structural constraint against which tertiary structure changes. When oxygen binds to the dissociated dimer, it does not produce a tertiary structural change since there is no interface to oppose the ligand. This strained tertiary conformation raises the energy by +3 kcal/mol. The second conformational change produces a global quaternary change, as the salt bridges break and the T state changes to the R state.

The formation and release of the tertiary constraint is the driving force of cooperative ligand binding. The strength of the T interface is overcome ony when unfavorable ligand induced conformational changes occur in both dimers. The T interface can withstand 1 dimer with the changed tertiary conformation, not 2. The movement of Fe into the plane of the heme ring triggers the tertiary change. The trigger for the quaternary change is the tertiary changes in the dimers.