We have studied macromolecule structure. Now it is time to impart function to these molecules. It is simple
to imagine that before these molecules can perform a function, they must interact with specific molecule(s) or ligand(s) in
their environment. In fact, binding and subsequent release of a ligand might be the sole function of the macromolecule (example
myoglobin binding oxygen). Binding is the first step necessary for a biological response (with the exception of
visual transduction in which photo-induced isomerization of rhodopsin initiates the response). To understanding binding,
we must consider the equilbria involved, how binding is affected by ligand and macromolecule concentration, and how to experimentally
analyze and interpret binding data and binding curves.
DERIVATIONS OF BINDING EQUATIONS AND GRAPHS
These derivations can be made and interpreted using simple principles from General Chemistry,
which you reviewed and strengthened in Analytical Chemistry, with some slight differences. Biochemists rarely talk about equilibrium
or association constants, but rather their reciprocals - the dissociation constants, Kd. For the reactions M +
L <====> ML, where M is free macromolecule, L is free ligand, and ML is macromolecule-ligand complex (which is held
together by intermolecular forces, not covalent forces), the Kd is given by
[M]eq[L]eq/[ML]eq.
Figure: M is free macromolecule, L is free ligand, and ML is macromolecule-ligand complex
Notice the unit of Kd is molarity, M. The lower the Kd (i.e. the higher the [ML] at any
given M and L, the tighter the binding. The higher the Kd, the looser the binding. Kd's for biological molecules are finely
tuned to their environments. They vary from about 1 mM (weak interactions) for some enzyme-substrate complex, to pM - fM levels.
Example of very tight, non-covalent interactions are for the avidin (an egg protein)-biotin (a vitamin) complex and thrombin
(enzyme initiating clotting)-hirudin (a leech salivary protein) complex.
M = macromolecule; L = ligand
For a simple equilibrium M + L <--> ML
where M = free macromolecule, L = free ligand, and ML = bound M and L (a complex)
3 equations can be written:
Equation 1 - Dissociation constant: K d = ([M]eq[L]eq)/[ML]eq = ([M][L])/[ML]
(units of molarity)
Equation 2 - Mass Balance of M: Mo = M + ML
Equation 3 - Mass Balance of L: Lo = L + ML
We would like to derive equations which give ML as a function of known or measurable values. The
Kd equations shows that ML depends on free M and free L. From Equations 1-3, two different and equally valid equations
can be derived for two different cases.
- Case 1: used either when you can readily measure free L or when experimental conditions
are such the Lo >> Mo, which is often encountered. Under these latter conditions, free L
= Lo, which you know without measuring it, simply by knowing how much total ligand was added to the system.
- Case 2 (more general): used when you don't know free L or haven't measured it, and you just
wish to calculate how much ML is present at equilibrium. These conditions imply that Lo is not >>
Mo. (If Lo >> Mo, we would know free L = Lo.)
EXPERIMENTAL CASE 1: USE THIS FORM OF THE EQUATION WHEN L IS MEASURABLE OR WHEN Lo
>> Mo (i.e. L= Lo)
Equation 4 - Substitute 2 into 1: K d = ([M][L])/[ML] = [Mo-ML][L])/[ML]
(ML)Kd = (Mo)L - (ML)L
(ML)Kd + (ML)L = (Mo)L
(ML)(Kd+L) = (Mo)L
Equation 5: ML = MoL/(Kd + L)
This equation is ALWAYS TRUE for the chemical equation written above. L is the free ligand
concentration at equilibrium. If Lo >> Mo, then the equations simplifies to:
Equation 6: ML = MoLo/(Kd + L), whose graph you should draw below.
Dividing Equation 5 by Mo gives the fractional saturation of the macromolecule M, where
Equation 7: Y = q = [ML]/Mo = L/(Kd + L)
where Y can vary from 0 (when L = 0) to 1 (when L >> Kd)
Draw a graph of Y vs L or Lo
GRAPH IS A HYPERBOLA
Equations 5/6 can be understood best by examining three cases:
ML = MoL/(Kd + L)
Case 1: L = 0
ML = 0
Case 2: L = Kd
ML = MoL/(L + L)= MoL/2L = Mo/2
which indicates that M is half saturated. In fact the operational definition of Kd is the ligand
concentration at which the M is half saturated.
Case 3: L >> Kd
ML = Mo
EXPERIMENTAL CASE 2 (more general): USE THIS FORM OF THE EQUATION WHEN FREE L IS
NOT KNOWN (such as when Lo is not >> Mo) OR YOU WISH TO CALCULATE ML FROM JUST Lo,
Mo AND KD
Equation 8 - Substitute 2 AND 3 into 1: K d = ([M][L])/[ML] = [Mo-ML][Lo-ML]/[ML]
(ML)Kd = (Mo - ML)(Lo - ML)
(ML)Kd = (Mo)(Lo) - (ML)(Lo) - (ML)(Mo)
+ (ML)2 or
Equation 9: (ML)2 - (Lo + Mo +Kd)(ML) + (Mo)(Lo)
= 0, which is of the form
ax2 + bx + c = 0, where
a = 1
b = - (Lo + Mo +Kd)
c = (Mo)(Lo)
which are all constants, and
x = {-b +/- (b2 - 4ac)1/2}/2a or
Equation 10: ML = {-(Lo+Mo+Kd) +/- ((Lo+Mo+Kd)2 - 4MoLo)1/2}/2
A graph of ML calculated from this formula vs free L (or Lo if Lo >>
Mo) give a
A HYPERBOLA
In the derivations, we came up with two equations for ML:
- one (Equation 5) using mass conservation on M, which gave: ML = MoL/[Kd +L]
- one (Equation 10) using mass conservation on M and L, which gave ML = quadratic equation as function of Mo, Lo, and Kd:
ML = {-(Lo+Mo+Kd) +/- ((Lo+Mo+Kd)2 - 4MoLo)1/2}/2
Both equations are valid. In the first you must known free L which is often Lo if Mo << Lo. In the second, you don't
need to know free M or L at all. At a given Lo and Mo, you can calculate ML, which should be the same ML you get from
the first equation if you know free L.
Equations 5 and 10 are useful in several circumstances. They can be used to
- calculate the concentration of ML if Kd, Mo, and L (for equation 5) or if Kd, Mo, and Lo
(for equation 10) are known. This is analogous to the use of the Henderson-Hasselbach equation to calculate the protonation
state (HA) and hence charge state of an acid at various pH values. In the former case we are measuring the concentration
of bound ligand (ML) and in the later case, the concentration of bound protons (HA).
- calculate Kd if ML, Kd, Mo, and L (for equation 5) or if ML, Mo, and Lo (for equation
10) are known. Techniques to extract the Kd from binding data will be discussed in the next chapter section.
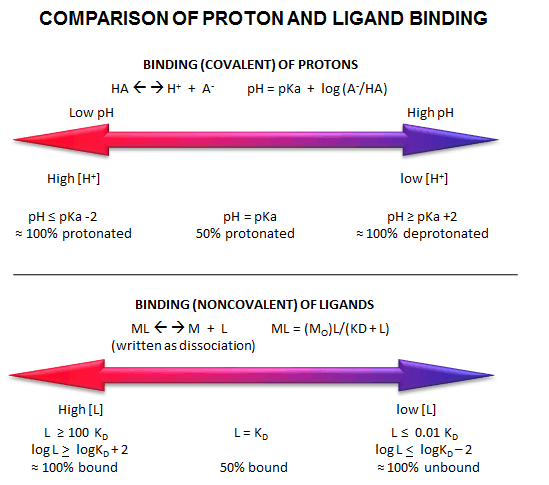
INTERPRETATION OF BINDING EQUATIONS AND GRAPHS
It is important to get a mathematical understanding of the binding equations and graphs. It is equally
important to get an intuitive understanding of their properties. Just as we used the +/- 2 rule in determining at a glance
the charge state of an acid, you need to be able to determine the extent of binding (how much of M is bound with L) given
their relative concentrations and the Kd. The usual situation is that the [Mo] is << [Lo]. What
happens to the binding curves for M + L <===> ML if the Kd gets progressively lower? Intuitively, you should expect
that binding will increase, especially as L gets greater. The curves below should help you develop the intuition you need
with respect to binding equilibria.
Fig: ML vs L at Varying Kd's
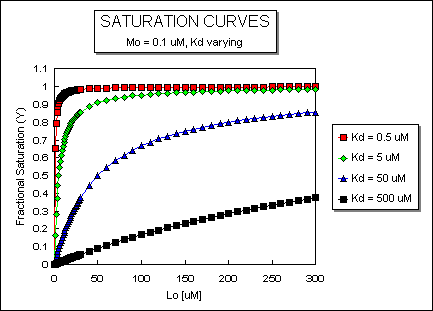
Fig: ML vs L at Even Lower Kd's
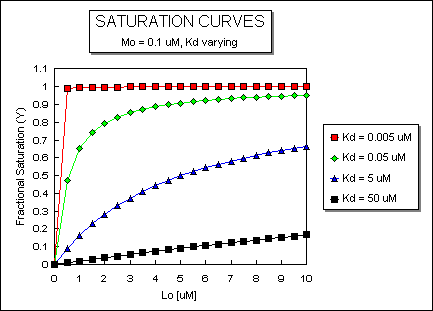
Fig: ML vs L at a Very Low Kd!
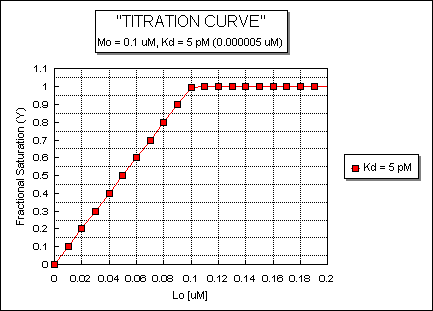
Fig: Comparison of Covalent Binding of Protons vs Noncovalent Binding of Ligand
HOW STRONG IS BINDING - THE CONTINUUM
Binding affinities give us a way to measure
the relative strength of binding between two substances. But how "tight" is tight binding? Weak binding? Let us exam that
issue by considering a binding continuum. Consider two substances, A and B that might interact. Over what range of strengths
can they actually bind to each other? It would helpful to set up the extremes of the binding continuum. At one end is
no binding at all. At the other end, consider two things that bind covalently. We have discussed how Kd reflects binding strength.
Remember, Kd = 1/Keq. Also, we know that Keq is related to DGo,
by the equations: DG o = -
R T ln Keq, or RT ln Kd. Given these simple equations, you should be able to interconvert between Keq, Kd, and DG o. (Keep your units straight.).
NO INTERACTION: One end of the binding continuum represents no interaction. Let's
assume that Keq is tiny (Kd large), for example Keq ~ 2.4 10-72. Plugging this into the equation DG o = - R T ln Keq, where R = 2.00 cal/mol.K,
and T is about 300K, the DGo ~
+100 kcal/mol. That is, if we add A + B, there is no drive to form AB. If AB did form, then it would immediately fall apart.
COVALENT INTERACTION: At the other end of the continuum consider the interaction
of 1H atom with another to form H2. From a general chemistry book we can get DGoform. Using General Chem. thermodynamics, we can calculate DGo for H-H formation. (DGo = SGoform
prod. - SGoform react.)
Doing this gives a value of -97 kcal/mol.
INTERMEDIATE REVERSIBLE INTERACTIONS: Consider the interaction of a protein, the
lambda repressor (R), with a small oligonucleotide to which it binds tightly (called the operator DNA, O). This is an example
of a biologically tight, but reversible interaction. R can bind to many short oligonucleotides due to electrostatic interactions
and H bonds from the positively charged protein to the negatively charge nucleic acid backbone. The tight binding interaction,
however, involves oligonucleotides of specific base sequence. Hence we can distinguish between tight binding, which usually
involves specific DNA sequence and weak binding which involves nonspecific sequences. Likewise, we will speak of specific
and nonspecific binding. R and O, which bind with a Kd of 1 pM, is an example of specific binding, while R and nonspecific
DNA (D), which bind mostly through electrostatic interactions with a Kd of 1 mM, is an example of nonspecific binding.
RATE CONSTANTS FOR ASSOCIATION AND DISSOCIATION: When the reaction
M + L <-===>
ML is at equilibrium, the rate of the forward reaction is equal to the rate of the reverse reaction. From General Chemistry,
the forward reaction is biomolecular and second order. Hence the vf, the rate in the forward direction is proportional
to [M][L], or
vf = kf [M][L], where kf is the rate constant in the forward direction.
The rate of the reverse reaction, vr is first order, proportional to [ML], and is given by vr = kr
[ML], where kr is the rate constant for the reverse reaction. Notice that the units of kf are M-1s-1,
while units of kr are s-1. At equilibrium, vf = vr, or kf [M][L] =
kr [ML]. Rearranging the equation gives [ML]/[M][L]= kf/ kr = Keq. Hence Keq is given by
the ratio of rate constants. For tight binding interactions, Keq >> 1, Kd << 1, and kf is very large
(in the order of 108-9 ) and kr must be very small (10-2 - 10 -4 s-1).
To get a more intuitive understanding of Kd's, it is often easier to think about the rate
constants which contribute to binding and dissociation. Let us assume that kr is the rate constant which
describes the dissociation reaction. It is often times called koff. It can be shown mathematically that the rate
at which two simple object associate depends on their radius and effective molecular weight. The maximal rate at which they
will associate is the maximal rate at which diffusion will lead them together. Let us assume that the rate at which M and
L associate is diffusion limited. The theoretical kon is about 108 M-1s-1. Knowing
this, the Kd and the fact that kon/ koff = Keq = 1/Kd, we can calculate koff, which remember
is a first order rate constant..
We can also determine k off experimentally. Imagine the following
example. Adjust the concentrations of M and L such that Mo << Lo and Lo>> Kd.
Under these conditions of ligand excess, M is entirely in the bound from, ML. Now at t = 0, dilute the solution so that
Lo << Kd. The only process that will occur here is dissociation, since negligible association can occur given
the new condition. If you can measure the biological activity of ML, then you could measure the rate of disappearance of ML
with time, and get koff. Alternatively, if you could measure the biological activity of M, the rate at which activity
returns will give you koff.
Now you will remember from General Chemistry that from a first order rate constant, the
half-life of the reaction can be calculated by the expression: k = 0.693/t1/2. Hence given koff, you
can determine the t1/2 for the associated species existence. That is, how long will a complex of ML last before
it dissociates? Given DGo or Kd, and
assuming a kon (108), you should be able to calculate koff and t1/2. Or, you could
be able to determine koff experimentally, and then calculate t1/2. Applying these principles, you can
calculate the parameters below.
Calculated
koff and t1/2 for binary complexes assuming diffusion-controlled kon
|
|
KD (M) |
koff (s-1) |
t ½ |
|
H2 |
1 x 10-71 |
1 x 10-63 |
2 x 1055 yr |
|
RtV3
: Rt'L3(a) |
10-17 |
1 x 10-9 |
2 yr |
|
Avidin:biotin |
10-15 |
1 x 10-7 |
80 days |
|
thrombin:hirudin(b) |
5 x10-14 |
5 x 10-6 |
2 days |
|
lacrep:DNAoper(c)
|
1 x 10-13 |
1 x 10-5 |
0.8 days |
|
Zif268:DNA(d) |
10-11 |
1 x 10-3 |
700 s |
|
GroEL:r-lactalbumin(e)
|
10-9 |
0.1 |
7 s |
|
TBP:TATA(f) |
2 x 10-9 |
2 x 10-1 |
3 s |
|
TBP:TBP |
4 x 10-9 |
4 x 10-1 |
2 s |
|
LDH (pig): NADH(g) |
7.1 x 10-7(j) |
7.1 x 101 |
10 ms |
|
profilin: CaATP-G-actin |
1.2 x 10-6 |
1.2 x 102 |
6 ms |
|
TBP: DNAnonspec(h)
|
5 x 10-6 |
5 x 102 |
1 ms |
|
TCR(i): cyto C peptide |
7X10-5 |
7X103 |
100 ms |
|
lacrep:DNAnonspec(h) |
1 x 10-4 |
1 X104 |
70 ms |
|
uridine-3P: RNase |
1.4 x 10-4 (j) |
1.4X10-4 |
50 ms |
|
Creatine Kinase: ADP |
8.2 x 10-4 (j) |
8.2X104 |
10 ms |
|
Acetylcholine:Esterase |
1.2 x 10-3 |
1.2 x 105 |
6 ms |
|
no interaction |
4 x 1073 |
4 x 1081 |
- |
-
Trivalent Vancomycin derivative RtV3 + Trivalent D-Ala-D-Ala deriv, Rt'L3'
-
Hirudin is a potent thrombin inhibitor from leach saliva
-
lac rep is the E. Coli lac operon repressor protein, and DNAoper
is the specific DNA binding region in the E. Coli genome that binds to the repressor
-
Zif268 is a mouse zinc-finger binding protein
-
GroEL is a chaperone protein; r-lactalbumin is the reduced form of lactalbumin
-
TBP is the TATA Binding Protein which binds to the TATA box consensus sequence
-
LDH is lactate dehydrogenase
-
DNAnonspec is DNA which does not contain the specific DNA sequence region involved in specific
binding
to a DNA binding protein
-
TCR is the T-cell receptor
-
calculated from equation: KD = koff/kon.
What is usually measured is Kd and/or koff (if the koff is reasonable).
This analysis is very simplified. Electrostatic forces and other orientation factors may significantly change kon,
while conformational changes in the complex may prevent ready unbinding of the bound ligand, dramatically altering koff.
EXPERIMENTAL DETERMINATION OF Kd
It is often important to determine the Kd for a ML complex, since given that number and the concentrations
of M and L in the system, we can predict if M is bound or not under physiological conditions. Again, this is important since
whether M is bound or free will govern its activity. The trick in determining Kd is to determine ML and L at equilibrium.
How can we differentiate free from bound ligand? The following techniques allow such a differentiation.
TECHNIQUES THAT REQUIRE SEPARATION OF BOUND FROM FREE LIGAND - Care must be given to ensure that the equilibrium
of M + L <==> ML is not shifted during the separation technique.
- gel filration chromatography - Add M to a given concentration of L. Then chromatograph
the mixture on gel filtration column eluting with the free ligand at the same concentration. The ML complex will elute first
and can be quantitated . If you measure the free ligand coming off the column, it will be constant after the ML elutes with
the exception of a single dip near where the free L would elute if the column was eluted without free L in the buffer solution.
This dip represents the amount of ligand bound by M.
- membrane filtration - Add M to radiolableled L, equilibrate, and then filter through a filter
which binds M and ML. For instance, a nitrocellulose membrane binds proteins irreversibly. Determine the amount of radiolabeled
L on the membrane which equals [ML].
- precipitation - Add a precipitating agent like ammonium sulfate, which precipitates proteins and
hence both M and ML. Determine the amount of ML.
TECHNIQUES THAT DO NOT REQUIRE SEPARATION OF BOUND FROM FREE LIGAND
- equilibirum dialysis - Place M in a dialysis bag and dialyse against a solution containing a ligand
whose concentration can be determined using radioisotopic or spectroscopic techniques. At equilibrium, determine free L by
sampling the solution surrounding the bag. By mass balance, determine the amount of bound ligand, which for a 1:1 stoichiometry
gives ML. Repeat at many different ligand concentrations
.
- spectroscopy - Find a ligand whose absorbance or fluorescence spectra changes when bound to M.
Alternatively, monitor a group on M whose absorbance or fluorescence spectra changes when bound to L.
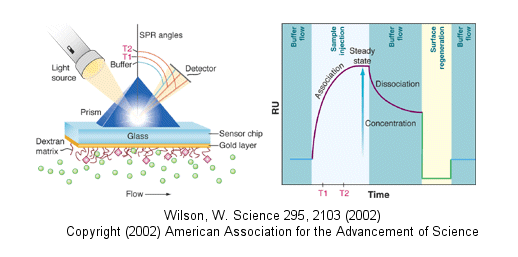
Surface Plasmon Resonance
A newer technique to measure binding is called surface plasmon resonance (SPR) using a sensor chip consisting
of a 50 nm layer of gold on a glass surface. A carbohydrate matrix is then added to the gold surface. To the CHO
matrix is attached through covalent chemistry a macromolecle which contains a binding site of a ligand. The binding
site on the macromolecule must not be perturbed to any significant extent. A liquid containing the ligand is flowed
over the binding surface.
The detection system consists of a light beam that passes through a prism on top of the glass layer.
The light is totally reflected but another component of the wave called an evanescent wave, passes into the gold layer,
where it can excite the Au electrons. If the correct wavelength and angle is chosen, a resonant wave of excited electrons
(plasmon resonance) is produced at the gold surface, decreasing the total intensity of the reflected wave. The angle
of the SPR is sensitive to the layers attached to the gold. Binding and dissociation of ligand is sufficient to change
the SPR angle, as seen in the figure below. (Science, 295, pg 2103 (2002))
Fig: Surface Plasmon Resonance
Amazing Binding Affinity of Metals to Protein: An Example
An incredibly tight binding interaction has recently been reported for the binding of Cu1+ to the CueR protein
from E. Coli. Cu1+ ions are usually kept to a very low concentration in cells as a mechanism to prevent
toxicity. Yet some enzymes require Cu. Free copper ions must be present in the cell to allow binding to appropriate
sites in proteins. How are these competing concerns regulated in the cell? The total Cu concentration in E. Coli is
about 10 mM, which, given the small size of the bacterium, represents about 10,000 copper ions per
cell.
Cells have evolved many mechanisms to control and deliver Cu ions. Copper ions can be delivered to target proteins
by copper chaperones (analogs of the chaperone proteins which guide protein folding). CueR in E. Coli appears to regulate
the copper-induced expression of genes involved in copper biochemistry (including an enzyme that oxidizes Cu1+
to Cu2+ which is less toxic). One particular gene that is upregulated is copA. CueR increases transcription
of copA in the presence of Cu, Ag, and Au (coinage metal) ions. Changela et al. developed an in vitro assay which determined
the extent of expression of CueR regulated genes, under a variety of ion types and concentrations. In the assay, purified
CueR was added to a gene construct containing the promoter for copA. Initially they found that transcription was always
on even in the presence of a ligand, glutathione, which binds Cu1+ avidly and should keep free Cu1+
levels very low. They switched to an even tighter binding Cu1+ coordinator, cyanide (CN-), to
reduce the free Cu1+ levels to even lower levels. Extremely high levels of CN- (millimolar) stopped
transcriptional activation, but if excess Cu1+ was added, activation ensued, suggesting that copper binding to
the protein was reversible. At 1 mM CN-, transcription increased with addition of copper ions up to a TOTAL
Cu1+ concentration of 60 mm. Under these condition, the free Cu1+ concentrations
were much less. Half-maximal activation occurred at a TOTAL Cu1+ concentration of 0.7
mM. Similar activation was observed by Ag1+ and Au1+, but not by Zn and Hg ions,
showing the specificity for monovalent cations over divalent cations.
Knowing the pKa of HCN, stability constants for Cu1+:CN- complexes, and CN- concentrations, Changela
et al produced a series of solutions buffered in FREE Cu1+ that extended from 10-18 to 10-23
M (pH 8.0). (For example, the log of the binding constant b, logb,
for the Cu1+ + 2CN- <==> [Cu(CN)2]- is 21.7. You solved problems such
as this involving linked equilibrium if you have taken analytical chemistry.) The free Cu1+ concentration
at half-maximal activation of gene reporter transcription, a measure of the dissociation constant, Kd, was approximately 1
x 10-21 M (zeptomolar)! Now assume that the volume of the contents of an E. Coli cell is 1.5 x 10-15
L. If there were only one ion of Cu1+ in the cell, it would have a concentration of 10-9 M.
The values suggest that there is no free Cu1+ ions in the cell, and that only 1 Cu+1 ion in the cell
is enough to ensure its binding to CueR and subsequent transcriptional activation of copA.
Molecular Basis of High Affinity (Low Kd) Binding Interactions
What differentiates how and low affinity binding at the molecular level? Do high affinity interactions
have lots of intramolecular H-bonds, salt bridges, van der Waals interactions, or are hydrophobic interactions most important?
Recently, the crystal structures of a variety of antibody-protein complexes were determined in order to study the basis of
affinity maturation of antibody molecules. It is well know that antibodies elicited on exposure to a foreign molecule
(antigen) are initially of lower affinity than antibodies released later in the immune response. An incredible
number of different antibodies can be made by antibody-producing B cells due to genetic mechanisms (combining different variable
regions of antibody genes through splicing, imprecise splicing, and hypermutation of critical nucleotides in the genes
of antigen binding regions of antibodies). Clones of antibody-producing cells with higher affinity are selected
through binding and clonal expansion of these cells. Investigators studied the crystal structure of 4 different antibodies
which bound to the same site (epitope) on the protein antigen lysozyme. Increased affinity was correlated with increased
buried apolar surface area and not with increased numbers of H bonds or salt bridges.
Table: Characteristics of Antibody:Hen Egg Lysozyme Complexes(HEL)
| Antibody |
H26-HEL |
H63-HEL |
H10-HEL |
H8-HEL |
| Kd (nM) |
7.14 |
3.60 |
0.313 |
0.200 |
| Intermolecular Interactions |
| H bonds |
24 |
25 |
20 |
23 |
| VDW contacts |
159 |
144 |
134 |
153 |
| salt bridges |
1 |
1 |
1 |
1 |
|
Buried Surface Area |
| DASURF (A2) |
1,812 |
1,825 |
1,824 |
1,872 |
| DASURF-polar (A2) |
1,149 |
1,101 |
1,075 |
1,052 |
| DASURF-apolar (A2) |
663 |
724 |
749 |
820 |
Li,Y. et al. Nature: Structural Biology. 6, pg 484 (2003)
 Online Lit: Antibodies with Infinite Affinity. Chmura et al. PNAS. 98, pg 8480 (1998)
Online Lit: Antibodies with Infinite Affinity. Chmura et al. PNAS. 98, pg 8480 (1998)
Docking
The quantitative methods described above do not elucidate the mechanism of binding. Computer programs
have been developed that allow the docking of a ligand (small molecule or even another protein) to another protein.
The automatic docking of flexible ligands to proteins can be modeled using Autodock. AutoDock contains the following programs:
-
AutoDock performs the docking of the ligand to a set of grids describing the target
protein;
-
AutoGrid pre-calculates these grids;
-
AutoTors sets up which bonds will treated as rotatable in the ligand.
Autodock 4 is set to be released in mid 2003, hopefully in time to incorporate
into class projects.
The Crowded Cell
Most binding studies are performed in vitro with dilution concentrations of both macromolecule and ligand.
Are these conditions illustrious of conditions inside a cell? The answer is no! Cells are very crowded with organelles,
macromolecular complexes, and cytoskeletal components which provide internal architecture to the cell, etc. Total macromolecule
concentration in the cell has been estimated to be as high as 400 g/1L = 400 g/1000 mL = 0.4 g/mL = 400 mg/mL. Try to
dissolve a water soluble protein like albumin to those concentrations! From 5 to 40% of the entire cellular volume is
occupied with large molecules, and at the upper range, very little space exists for other large macromolecules.

