|
Neurochemistry is one of the most explosive areas of biological research. Scientists are now starting
to unravel the molecular bases for memory, cognition, emotion, and behavior. The next decades will bring truly revolutionary
understanding of brain chemistry and along with it the potential to alter human mood, memory, and to treat mental illness
such as schizophrenia much more effectively. The human brain, with about 100 billion neurons (each which can form connections
- synapses - with 1000 to 10,000 other neurons ) and associated glial cells (10-50 times the number of neurons) can
be considered one of the most complex structures in the universe. This section will explore the biology and chemistry
of neurons.
 Brain Brain
| Average Brain Weights (in grams) |
| Species |
Weight (g) |
 |
Species |
Weight (g) |
| adult human |
1,300 - 1,400 |
 |
newborn human |
350 - 400 |
| sperm whale |
7,800 |
 |
fin whale |
6,930 |
| elephant |
6,000 |
 |
humpback whale |
4,675 |
| gray whale |
4,317 |
 |
killer whale |
5,620 |
| bowhead whale |
2,738 |
 |
pilot whale |
2,670 |
| bottle-nosed dolphin |
1,500 - 1,600 |
 |
walrus |
1,020 - 1,126 |
| Pithecanthropus Man |
850 - 1,000 |
 |
camel |
762 |
| giraffe |
680 |
 |
hippopotamus |
582 |
| leopard seal |
542 |
 |
horse |
532 |
| polar bear |
498 |
 |
gorilla |
465 - 540 |
| cow |
425-458 |
 |
chimpanzee |
420 |
| orangutan |
370 |
 |
California sea lion |
363 |
| manatee |
360 |
 |
tiger |
263.5 |
| lion |
240 |
 |
grizzly bear |
234 |
| sheep |
140 |
 |
baboon |
137 |
| adult rhesus monkey |
90-97 |
 |
dog (beagle) |
72 |
| aardvark |
72 |
 |
beaver |
45 |
| shark (great white) |
34 |
 |
shark (nurse) |
32 |
| cat |
30 |
 |
porcupine |
25 |
| squirrel monkey |
22 |
 |
marmot |
17 |
| rabbit |
10-13 |
 |
platypus |
9 |
| alligator |
8.4 |
 |
squirrel |
7.6 |
| opossum |
6 |
 |
flying lemur |
6 |
| fairy anteater |
4.4 |
 |
guinea pig |
4 |
| ring-necked pheasant |
4.0 |
 |
hedgehog |
3.35 |
| tree shrew |
3 |
 |
fairy armadillo |
2.5 |
| owl |
2.2 |
 |
grey partridge |
1.9 |
| rat (400 g body weight) |
2 |
 |
hamster |
1.4 |
| elephant shrew |
1.3 |
 |
house sparrow |
1.0 |
| european quail |
0.9 |
 |
turtle |
0.3-0.7 |
| bull frog |
0.24 |
 |
viper |
0.1 |
| goldfish |
0.097 |
 |
green lizard |
0.08 |
Reference for many of these brain weights:
- Blinkov, S.M. and Glezer, I.I. The Human Brain in Figures and Tables. A Quantitative Handbook, New York: Plenum
Press, 1968.
- Demski, L.S. and Northcutt, R.G. The brain and cranial nerves of the white shark: an evolutionary perspective. In Great
White Sharks. The Biology of Carcharodon carcharias, San Diego: Academic Press, 1996.
- Nieuwenhuys, R., Ten Donkelaar, H.J. and Nicholson, C. The Central Nervous System of Vertebrates. Vol. 3, Berlin:
Springer, 1998.
- Berta, A., et al. Marine Mammals. Evolutionary Biology, San Diego: Academic Press, 1999.
- Mink, J.W., Blumenschine, R.J. and Adams, D.B. Ratio of central nervous system to body metabolism in vertebrates: its
constancy and functional basis. Am. J. Physiology, 241:R203-R212, 1981.
- Rehkamper, G., Frahm, H.D. and Zilles, K. Quantitative development of brain and brain structures in birds (Galliformes
and Passeriforms) compared to that in mammals (Insectivores and Primates). Brain Beh. Evol., 37:125-143, 1991.
- Ridgway, S.H. and Harrison, S., Handbook of Marine Mammals, Vol. 3, London: Academic Press, 1985.
|
% brain of total body weight (150 pound human) = 2%
Average brain width = 140 mm
Average brain length = 167 mm
Average
brain height = 93 mm
Intracranial contents by volume (1,700 ml, 100%): brain = 1,400 ml (80%); blood = 150 ml (10%); cerebrospinal fluid = 150
ml (10%) (from Rengachary, S.S. and Ellenbogen, R.G., editors, Principles of Neurosurgery, Edinburgh:
Elsevier Mosby, 2005)
Average number of neurons in the brain = 100 billion
Number of neurons in brain (octopus) = 300 million (from How Animals See, S. Sinclair, 1985)
Number of neurons in Aplysia nervous system = 18,000-20,000
Number
of neurons in each segmental ganglia in the leech = 350
Volume of the brain of a locust = 6mm3 (from The Neurobiology of the Insect Brain, Burrows, M., 1996)
Ratio of the volume of grey matter to white matter in the cerebral hemipheres (20 yrs. old) = 1.3 (Miller,
A.K., Alston, R.L. and Corsellis, J.A., Variation with age in the volumes of grey and white matter in the cerebral hemispheres
of man: measurements with an image analyser, Neuropathol Appl Neurobiol., 6:119-132, 1980)
Ratio of the
volume of grey matter to white matter in the cerebral hemipheres (50 yrs. old) = 1.1 (Miller et al., 1980)
Ratio of the
volume of grey matter to white matter in the cerebral hemipheres (1000 yrs. old) = 1.5 (Miller et al., 1980)
% of cerebral
oxygen consumption by white matter = 6%
% of cerebral oxygen consumption by gray matter = 94%
Average number of glial cells in brain = 10-50 times the number of neurons
(For more information about the number of neurons in the brain, see R.W. Williams and K. Herrup, Ann. Review Neuroscience,
11:423-453, 1988)
Number of neocortical neurons (females) = 19.3 billion (Pakkenberg, B., Pelvig, D., Marner,L., Bundgaard,
M.J., Gundersen, H.J.G., Nyengaard, J.R. and Regeur, L. Aging and the human neocortex. Exp. Gerontology, 38:95-99, 2003 and
Pakkenberg, B. and Gundersen, H.J.G. Neocortical neuron number in humans: effect of sex and age. J. Comp. Neurology, 384:312-320,
1997.)
Number of neocortical neurons (males) = 22.8 billion (Pakkenberg et al., 1997; 2003)
Average loss of neocortical
neurons = 85,000 per day (~31 million per year) (Pakkenberg et al., 1997; 2003)
Average loss of neocortical neurons = 1
per second (Pakkenberg et al., 1997; 2003)
Average number of neocortical glial cells (young adults ) = 39 billion (Pakkenberg
et al., 1997; 2003)
Average number of neocortical glial cells (older adults) =36 billion (Pakkenberg et al., 1997; 2003)
Length
of myelinated nerve fibers in brain = 150,000-180,000 km (Pakkenberg et al., 1997; 2003)
Number of synapses in cortex =
0.15 quadrillion (Pakkenberg et al., 1997; 2003)
Difference number of neurons in the right and left hemispheres = 186 million
MORE neurons on left side than right side (Pakkenberg et al., 1997; 2003)
 |
Proportion by Volume (%) |
 |
Rat |
Human |
| Cerebral Cortex |
31 |
77 |
| Diencephalon |
7 |
4 |
| Midbrain |
6 |
4 |
| Hindbrain |
7 |
2 |
| Cerebellum |
10 |
10 |
| Spinal Cord |
35 |
2 |
| (Reference: Trends in Neuroscience, November 1995) |
| Composition of Brain and Muscle |
 |
Skeletal Muscle (%) |
Whole Brain (%) |
| Water |
75 |
77 to 78 |
| Lipids |
5 |
10 to 12 |
| Protein |
18 to 20 |
8 |
| Carbohydrate |
1 |
1 |
| Soluble organic substances |
3 to 5 |
2 |
| Inorganic salts |
1 |
1 |
| (Reference: McIlwain, H. and Bachelard, H.S., Biochemistry and the Central Nervous System, Edinburgh:
Churchill Livingstone, 1985) |
Total surface area of the cerebral cortex = 2,500 cm2 (2.5 ft2; A. Peters, and E.G.
Jones, Cerebral Cortex, 1984)
Total surface area of the cerebral cortex (lesser shrew) = 0.8 cm2
Total surface area of the cerebral cortex
(rat) = 6 cm2
Total surface area of the cerebral cortex (cat) = 83 cm2
Total surface area of the
cerebral cortex (African elephant) = 6,300 cm2
Total surface area of the cerebral cortex (Bottlenosed dolphin)
= 3,745 cm2 (S.H. Ridgway, The Cetacean Central Nervous System, p. 221)
Total surface
area of the cerebral cortex (pilot whale) = 5,800 cm2
Total surface area of the cerebral cortex (false killer
whale) = 7,400 cm2
(Reference for surface area figures: Nieuwenhuys, R., Ten Donkelaar, H.J. and
Nicholson, C., The Central nervous System of Vertebrates, Vol. 3, Berlin: Springer, 1998)
Total number of
neurons in cerebral cortex = 10 billion (from G.M. Shepherd, The Synaptic Organization of the Brain,
1998, p. 6). However, C. Koch lists the total number of neurons in the cerebral cortex at 20 billion (Biophysics
of Computation. Information Processing in Single Neurons, New York: Oxford Univ. Press, 1999, page 87).
Total number
of synapses in cerebral cortex = 60 trillion (yes, trillion) (from G.M. Shepherd, The Synaptic Organization of the Brain,
1998, p. 6). However, C. Koch lists the total synapses in the cerebral cortex at 240 trillion (Biophysics of Computation.
Information Processing in Single Neurons, New York: Oxford Univ. Press, 1999, page 87).
Percentage of total cerebral cortex volume (human): frontal lobe = 41%; temporal lobe = 22%; parietal lobe = 19%; occipital
lobe = 18%. (Caviness Jr., et al. Cerebral Cortex, 8:372-384, 1998.)
Number of cortical layers = 6
Thickness of cerebral cortex = 1.5-4.5 mm
Thickness of cerebral cortex (Bottlenosed
dolphin) = 1.3-1.8 mm (S.H. Ridgway, The Cetacean Central Nervous System, p. 221)
EEG - beta wave frequency = 13 to 30 Hz
EEG - alpha wave frequency = 8 to 13 Hz
EEG - theta wave frequency = 4 to
7 Hz
EEG - delta wave frequency = 0.5 to 4 Hz
World record, time without sleep = 264 hours (11 days) by Randy Gardner
in 1965. Note: In Biopsychology (by J.P.J. Pinel, Boston: Allyn and Bacon,
2000, p. 322), the record for time awake is attributed to Mrs. Maureen Weston. She apparently spent 449 hours [18 days, 17
hours] awake in a rocking chair. The Guinness Book of World Records [1990] has the record belonging to Robert McDonald
who spent 453 hours, 40 min in a rocking chair.
Time until unconsciousness after loss of blood supply to brain =
8-10 sec
Time until reflex loss after loss of blood supply to brain = 40-110 sec
Rate of neuron growth (early pregnancy) = 250,000 neurons/minute
Length of spiny terminals of a Purkinje cell = 40,700
micron
Number spines on a Purkinje cell dendritic branchlet = 61,000
Surface area of cerebellar cortex = 50,000 cm2
(from G.M. Shepherd, The Synaptic Organization of the Brain, 1998, p. 255)
Weight of adult
cerebellum = 150 grams (Afifi, A.K. and Bergman, R.A., Functional Neuroanatomy, New York: McGraw-Hill,
1998)
Number of Purkinje cells = 15-26 million
Number of synapses made on a Purkinje cell = up to 200,000
Weight
of hypothalamus = 4 g
Volume of suprachiasmatic nucleus = 0.3 mm3
Number of fibers in pyramidal tract above
decussation = 1,100,000
Number of fibers in corpus callosum = 250,000,000
Area of the corpus callosum (midsagittal section) = 6.2 cm2
| Species |
Cerebellum Weight (grams) |
Body Weight (grams) |
| Mouse |
0.09 |
58 |
| Bat |
0.09 |
30 |
| Flying Fox |
0.3 |
130 |
| Pigeon |
0.4 |
500 |
| Guinea Pig |
0.9 |
485 |
| Squirrel |
1.5 |
350 |
| Chinchilla |
1.7 |
500 |
| Rabbit |
1.9 |
1,800 |
| Hare |
2.3 |
3,000 |
| Cat |
5.3 |
3,500 |
| Dog |
6.0 |
3,500 |
| Macaque |
7.8 |
6,000 |
| Sheep |
21.5 |
25,000 |
| Bovine |
35.7 |
300,000 |
| Human |
142 |
60,000 |
| Source: Sultan, F. and Braitenberg, V. Shapes and sizes of different mammalian cerebella. A study in quantitative
comparative neuroanatomy. J. Hirnforsch., 34:79-92, 1993. |
Total volume of cerebrospinal fluid = 125-150 ml
Half life of cerebrospinal fluid = 3 hours
Daily production of CSF
= 400 to 500 ml
Specific gravity of cerebrospinal fluid = 1.007
Color of normal CSF = clear and colorless
White Blood
cell count in CSF = 0-3 per mm3
Red Blood cell count in CSF = 0-5 per mm3
Normal intracranial
pressure = 150 - 180 mm of water
| Composition of Serum and Cerebrospinal Fluid (CSF) |
 |
CSF |
Serum |
| Water (%) |
99 |
93 |
| Protein (mg/dl) |
35 |
7000 |
| Glucose (mg/dl) |
60 |
90 |
| Osmolarity (mOsm/l) |
295 |
295 |
| Na (meq/l) |
138 |
138 |
| K (meq/l) |
2.8 |
4.5 |
| Ca (meq/l) |
2.1 |
4.8 |
| Mg (meq/l) |
0.3 |
1.7 |
| Cl (meq/l) |
119 |
102 |
| pH |
7.33 |
7.41 |
| (Reference: Fishman, R.A. Cerebrospinal Fluid in Disease of the Nervous System. Philadelphia: Saunders, 1980)
|
 Number of cranial nerves = 12 Number of cranial nerves = 12
I- olfactory
II- optic
Number of fibers in human optic nerve = 1,200,000
Number of fibers in cat optic nerve = 119,000
Number of
fibers in albino rat optic nerve = 74,800
Length of optic nerve = 50 mm
III- oculomotor
Number of fibers in oculomotor nerve = 25,000-35,000
IV- trochlear
Number of fibers in trochlear nerve = 2,000-3,500
Number of neurons in nucleus of the trochlear nerve = 2,000-3,500
V- trigeminal
Number of fibers in motor root of trigeminal nerve = 8,100
Number of fibers in sensory root of trigeminal nerve
= 140,000
VI- abducens
Number of fibers in abducens nerve (at exit from brain stem) = 3,700
VII- facial
Number of fibers in facial nerve (at exit from brain stem) = 9,000-10,000
Length of nucleus of the facial nerve
= 2 to 5.6 mm
Number of neurons in nucleus of the facial nerve = 7,000
VIII-vestibulocochlear
IX- glossopharyngeal
X- vagus
Length of dorsal motor nucleus of the vagus nerve = 10 mm
XI- spinal accessory
XII- hypoglossal
Number of neurons in nucleus of the hypoglossal nerve = 4,500-7,500
Length of nucleus of the hypoglossal nerve
= 10 mm
 Spinal Cord Spinal Cord
Number of neurons in human spinal cord = 1 billion (from Kalat, J.W., Biological Psychology, 6th Edition, 1998,
page 24)
Length of human spinal cord = 45 cm (male); 43 cm (female)
Length of human vertebral column = 70 cm
Length
of cat spinal cord = 34 cm
Length of rabbit spinal cord = 18 cm
Weight of human spinal cord = 35 g
Weight of rabbit spinal cord = 4 g
Weight of rat spinal cord (400 g body weight)
= 0.7 g
Maximal Circumference of cervical enlargement = 38 mm
Maximal Circumference of lumbar enlargement = 35 mm
Pairs
of Spinal Nerves = 31
Number of Spinal Cord segments = 31
8 cervical segments
12 thoracic segments
5 lumbar segments
5 sacral segments
1 coccygeal segment
 Sensory Apparatus Sensory Apparatus
Audition
Surface area of the tympanic membrane = 85mm2 (Hearing. Its Physiology and Pathophysiology,
A.R. Moller, San Diego, Academic Press, 2000)
Length of the eustachian tube = 3.5 to 3.9 cm (Hearing.
Its Physiology and Pathophysiology, A.R. Moller, San Diego, Academic Press, 2000.)
Number of hair cells in cochlea
= 3,500 inner hair cells; 12,000 outer hair cells (Hearing. Its Physiology and Pathophysiology, A.R.
Moller, San Diego, Academic Press, 2000.)
Number of fibers in auditory nerve = 28,000-30,000
Length of auditory
nerve = 2.5 cm
Number of neurons in cochlear nuclei = 8,800 (Northern, J.L. and Downs, M.P., Hearing in Children,
5th edition, Philadelphia: Lippincott Williams & Wilkins, 2002.)
Number of neurons in inferior colliculus =
392,000 (Northern, J.L. and Downs, M.P., Hearing in Children, 5th edition, Philadelphia: Lippincott Williams
& Wilkins, 2002.)
Number of neurons in medial geniculate body = 570,000
Number of neurons in auditory cortex
= 100,000,000
Hearing Range (young adult human) = 20 to 20,000 Hz
Hearing Range (elderly human) = 50 to 8,000 Hz (Guyton, A.C., Textbook of Medical Physiology, 1986)
Hearing Range (rat) = 1,000 to 50,000 Hz
Hearing
Range (cat) = 100 to 60,000 Hz
Hearing Range (dolphin) = 200 to 150,000 Hz
Hearing Range (elephant) = 1 to 20,000 Hz
Hearing
Range (goldfish) = 5 to 2,000 Hz
Hearing Range (moth, noctuid) = 1,000 to 240,000 Hz
Hearing Range (mouse) = 1,000 to
100,000 Hz
Hearing Range (sea lion) = 100 to 40,000 Hz
(Hearing range reference: Discover Science Almanac,
New York: Hyperion, 2003)
Most sensitive range of human hearing = 1,000-4,000 Hz
Length of external auditory
meatus (ear canal) = 2.7 cm
Diameter of external auditory meatus (ear canal)= 0.7 cm
Weight of malleus = 23 mg; length of malleus = 8-9 mm
Weight
of incus = 30 mg; dimensions of incus = 5 mm by 7 mm
Weight of stapes = 3-4 mg; dimensions of stapes = 3.5 mm high, 3 mm
long, 1.4 mm wide
Malleus, incus and stapes references: Gelfand, S.A. Hearing: An Introduction to Psychological
and Physiological Acoustics, 4th edition, New York: Marcel Dekker, 2004.
Length of cochlea = 35 mm
Width of cochlea = 10 mm
Number of turns in the cochlea = 2.2-2.9
Length of basilar
membrane = 25-35 mm
Width of basilar membrane = 150 microns (at base of cochlea) (Hearing. Its Physiology
and Pathophysiology, A.R. Moller, San Diego, Academic Press, 2000.)
Auditory Pain Threshold = 130 db
Threshold
for hearing damage = 90 db for an extended period of time
| Decibel Sound Scale |
| Decibels |
Sound |
| 180 |
Rocket launching pad |
| 140 |
Jet plane |
| 140 |
Gunshot blast |
| 120 |
Automobile horn |
| 130 |
Pain threshold |
| 120 |
Discomfort |
| 90 |
Subway |
| 80 |
Noisy Restaurant |
| 75 |
Busy traffic |
| 66 |
Normal conversation |
| 50 |
Average home |
| 30 |
Soft whisper |
| Source: Lee, K.J., Essential Otolaryngology, 8th edition, New York: McGraw-Hill,
2003. |
Taste
Total number of human taste buds (tongue, palate, cheeks) = 10,000
Number of taste buds on the tongue = 9,000
Height
of taste bud = 50-100 microns (From: Farbman, A.I., Taste Bud, in G. Adelman, eds., Encyclopedia of Neuroscience,
1987)
Diameter of taste bud = 30-60 microns (From: Farbman, A.I.)
Number of receptors on
each taste bud = 50-150 (Boron, W.F. and Boulpaep, E.L., Medical Physiology. A Cellular and Molecular Approach,
Philadelphia: Saunders, 2003)
Diameter of taste receptor = 10 micron
Diameter of taste fiber = less than 4 micron
Taste
threshold for quinine sulfate = 3.376 mg/liter water
Smell
Number of human olfactory receptor cells = 12 million (Shier, D., Butler, J. and Lewis, R. Hole's
Human Anatomy & Physiology, Boston: McGraw Hill, 2004)
Number of rabbit olfactory receptor cells
= 100 million
Number of dog olfactory receptor cells = 1 billion
Number of bloodhound olfactory receptor
cells = 4 billion (Shier, D., Butler, J. and Lewis, R. Hole's Human Anatomy & Physiology, Boston:
McGraw Hill, 2004)
Surface area of olfactory epithelium (contains olfactory receptor cells) in humans = 10 cm2
(Bear, M.F., Connors, B.W. and Pradiso, M.A., Neuroscience: Exploring the Brain, 2nd edition, Baltimore: Lippincott
Williams and Wilkins, 2001, p. 269)
Surface area of bloodhound olfactory epithelium = 59 in2 (Shier,
D., Butler, J. and Lewis, R. Hole's Human Anatomy & Physiology, Boston: McGraw Hill, 2004)
Area of olfactory
epithelium in some dogs = 170 cm2 (Bear, M.F., Connors, B.W. and Pradiso, M.A., Neuroscience: Exploring the Brain,
2nd edition, Baltimore: Lippincott Williams and Wilkins, 2001, p. 269)
Area of olfactory epithelium in cats = 21 cm2
(Bradshaw, J., Behavioral biology, in The Waltham Book of Dog and Cat Behaviour, ed. C. Thorne, Oxford:
Pergamon Press, 1992)
Thickness of olfactory epithelium mucous layer = 20-50 microns. (Boron and Boulpaep,
2003)
Diameter of olfactory receptor axons = 0.1-0.2 micron
Diameter of distal end olfactory receptor cell =
1 micron
Diameter of olfactory receptor cell = 40-50 micron
Number of cilia per olfactory receptor cell = 10-30
Length
of cilia on olfactory receptor cell = 100-150 micron
Concentration for detection threshold of musk = 0.00004 mg/liter air
Vision
Length of eyeball = 24.5 mm (from Spaide, R.F., 1999)
Volume of eyeball = 5.5 cm3
Weight
of eyeball = 7.5 g
Average time between blinks = 2.8 seconds
Average duration of a single blink = 0.1-0.4 seconds (Schiffman, H.R., Sensation and Perception. An Integrated Approach, New York: John Wiley and Sons, Inc., 2001)
Thickness
of cornea = 0.54 mm in center; 0.65 in periphery
Diameter of cornea = 11.5 mm
Thickness of lens = 4 mm
Diameter of
lens = 9 mm
Composition of lens = 65% water; 35% protein
Number of retinal receptor cells = 5-6 million cones; 120-140
million rods
Number of retinal ganglion cells = 800 thousand to 1 million
Number of fibers in optic nerve = 1,200,000
Number
of neurons in lateral geniculate body = 570,000
Number of cells in visual cortex (area 17) = 538,000,000
Wavelength
of visible light (human) = 400-700 nm
Amount of light necessary to excite a rod = 1 photon
Amount of light necessary
to excite a cone = 100 photons
Location of the greatest density of rods = 20o from fovea
Highest density
of rods = 160,000 per mm2
Peak density of rods (cat) = 400,000 per mm2
Density of cones in fovea
= 200,000 per mm2
Diameter of fovea = 1.5 mm
Intraocular pressure = 10-20 mm Hg
Volume of orbit = 30 ml
Area
of retina = 2,500 mm2
Thickness of retina = 120 microns (ranges from 100 to 230 microns)
Production rate
of aqueous humor = 2 microliters/min
Turnover of aqueous humor = 15 times/day
% volume of eye occupied by the vitreous
= 80%
Maximal sensitivity of red cones = 570 nm
Maximal sensitivity of green cones = 540 nm
Maximal sensitivity of
blue cones = 440 nm
More Facts and Figures about the Human Retina from WebVision.
Touch
Weight of skin (adult human) = 9 lb.(4.1 kg) (Source: Schiffman, H.R., Sensation and Perception. An Integrated
Approach, New York: John Wiley and Sons, Inc., 2001)
Surface area of skin (adult human) = 3,000 in2
(~1.8 m2) (Source: Schiffman, H.R., Sensation and Perception. An Integrated Approach, New
York: John Wiley and Sons, Inc., 2001)
Number of tactile receptors in the hand = 17,000
Number of nerve endings
in hand = 1,300 per in2
von Frey threshold (Face) = 5 mg
2 point threshold (Finger) = 2-3 mm
Length of
Meissner corpuscle = 90 - 120 micron
Density of receptors on finger tips = 2,500 per cm2
Density of Meissner's
corpuscles on finger tips = 1,500 per cm2
Density of Merkel's cells on finger tips = 750 per cm2
Density
of Pacinian corpuscles on finger tips = 75 per cm2
Density of Ruffini's corpuscles on finger tips = 75 per cm2
Thermal
pain threshold = 45oC
 Neurons Neurons
Mass of a large sensory neuron = 10-6gram (from Groves and Rebec, Introduction to Biological
Psychology, 3rd edition, Dubuque: Wm.C. Brown Publ., 1988)
Number of synapses for a "typical" neuron = 1,000
to 10,000
Diameter of neuron = 4 micron (granule cell) to 100 micron (motor neuron in cord)
Diameter of neuron nucleus
= 3 to 18 micron
Length of Giraffe primary afferent axon (from toe to neck) = 15 feet
Resting potential of squid giant
axon = -70 mV
Conduction velocity of action potential = 0.6-120 m/s (1.2-250 miles/hr)
Single sodium pump maximum transport rate = 200 Na ions/sec; 130 K ions/sec
Typical number of sodium pumps = 1000 pumps/micron2
of membrane surface (from Willis and Grossman, Medical Neurobiology, Mosby, St. Louis, 1981, p. 36)
Total
number of sodium pumps for a small neuron = 1 million
Density of sodium channels (squid giant axon) = 300 per micron2
(from Hille, B., Ionic Channels of Excitable Membranes, Sinauer, Sunderland, 1984, p. 210.)
Number
of voltage-gated sodium channels at each node = 1,000 to 2,000 per micron2 (from Nolte, J., The
Human Brain, Mosby, 1999, p. 163.)
Number of voltage-gated sodium channels between nodes = 25 per micron2
(from Nolte, J., The Human Brain, Mosby, 1999, p. 163.)
Number of voltage-gated sodium channels
in unmyelinated axon = 100 to 200 per micron2 (from Nolte, J., The Human Brain, Mosby, 1999,
p. 163.)
Diameter of microtubule = 20 nanometer
Diameter of microfilament = 5 nanometer
Diameter of neurofilament
= 10 nanometer
Thickness of neuronal membrane = 5 nanometer
Thickness of squid giant axon membrane = 50-100 A
Membrane
surface area of a typical neuron = 250,000 um2 (Bear et al., 2001)
Membrane surface area of 100 billion neurons
= 25,000 m2, the size of four soccer fields (Bear, M.F., Connors, B.W. and Pradiso, M.A., Neuroscience: Exploring
the Brain, 2nd edition, Baltimore: Lippincott Williams and Wilkins, 2001, p. 97)
Typical synaptic cleft distance = 20-40 nanometers across (from Kandel et al., 2000, p. 176)
%
neurons stained by Golgi method = 5%
Slow axoplasmic transport rate = 0.2-4 mm/day (actin, tubulin)
Intermediate axoplasmic transport rate = 15-50
mm/day (mitochondrial protein)
Fast axoplasmic transport rate = 200-400 mm/day (peptides, glyolipids)
Number of molecules
of neurotransmitter in one synaptic vesicle = 5,000 (from Kandel et al., 2000, p. 277)
Diameter of
synaptic vesicle = 50 nanometer (small); 70-200 nanometer (large)
Diameter of neurofilament = 7 - 10 nm
Diameter of
microtubule = 25 nm
Internodal Length = 150 - 1500 microns (depends on fiber diameter
% composition of myelin = 70-80%
lipid; 20-30% protein
====================================
| Ion Concentration (mM) - SQUID NEURON |
 |
Intracellular |
Extracellular |
| Potassium |
400 |
20 |
| Sodium |
50 |
440 |
| Chloride |
40-150 |
560 |
| Calcium |
0.0001 |
10 |
 |
| Ion Concentration (mM) - MAMMALIAN NEURON |
 |
Intracellular |
Extracellular |
| Potassium |
140 |
5 |
| Sodium |
5-15 |
145 |
| Chloride |
4-30 |
110 |
| Calcium |
0.0001 |
1-2 |
| Data from Purves et al., Neuroscience, Sunderland: Sinauer Associates, 1997. |
====================================
Neurotoxins
 Blood Supply Blood Supply
% brain utilization of total resting oxygen = 20%
% blood flow from heart to brain = 15-20% (Kandel et
al., 2000)
Blood flow through whole brain (adult) = 750 ml/min
Blood flow through whole brain (adult) = 54 ml/100
g/min
Blood flow through whole brain (child) = 105 ml/100 g/min
Cerebral blood flow = 55 to 60 ml/100 g brain tissue/min
Cerebral
blood flow (gray matter) = 75 ml/100 g brain tissue/min
Cerebral blood flow (white matter) = 45 ml/100 g brain tissue/min
(Rengachary, S.S. and Ellenbogen, R.G., editors, Principles of Neurosurgery, Edinburgh: Elsevier Mosby,
2005)
Oxygen consumption whole brain = 46 cm3/min
Oxygen consumption whole brain = 3.3 ml/100 g/min
Blood
flow rate through each internal carotid artery = 180 ml/min
Blood flow rate through basilar artery = 380 ml/min
Diameter
of vertebral artery = 2-3 mm
Diameter of common carotid artery (adult) = 6 mm
Diameter of common carotid artery (newborn)
= 2.5 mm
THE RESTING POTENTIAL AND ACTION POTENTIALS
We will discuss two kinds of neurons - those that interact with muscles at the neuromuscular junction
and those that interact with other neurons in the central nervous system. Neurons consist of a single, nucleated cell
body with multiple signal-receiving outgrowths (dendrites) and multiple-signal sending outgrowths (axons) which end in a terminal
button. These interact through the synapse with dendrites on other neurons.
Figure: Neurons
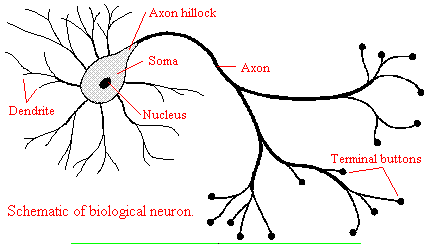
A presynaptic neuron can stimulate an adjacent postsynaptic neuron by releasing a neurotransmitter into
the synapse between the cells, which binds to a receptor in the membrane of the post-synapatic cell, stimulating the cell.
Figure: neurotransmitter into the synapse between the cells

We will discuss the events which cause the post-synaptic cell to "fire", but we will not discuss the immediate
events which lead to the release of neurotransmitter by the presynaptic neuron.
Neurons (as do all cells) have a transmembrane potential across the membrane. Transient changes in the
membrane potential are associated with neuron activation or inhibition. This arises in part due to the imbalance of
ions across the membrane which was established by the Na+-K+-ATPase in the membrane. This electrogenic
antiporter transfers 3 Na ions out of the cytoplasm for every 2 K ions it transports in. Likewise Cl- has a much
higher level outside the cell. Membrane potentials are determined not only by the size of the ion gradients across the
membrane, but also the differential permeability of membranes to ions. As we saw previously, synthetic bilayer membranes are not very permeable to ions .
Ion permeability of phosphatidyl serine vesicles
| ION |
PERMEABILITY (cm/s) |
| sodium |
<1.6 x 10-13 (lowest) |
| potassium |
<9 x 10-13 |
| chloride |
<1.5 x 10-11 (highest) |
Sodium would be expected to have a lower permeability than potassium since it has a higher charge density.
It also is largest in effective size due to the larger hydration sphere around the ion arising from its higher charge density.
Chloride would be expected to have the highest permeability since it has the lowest charge density (due to repulsion
of the electron cloud in the negative ion). Intracellular charged proteins (which are mostly negative) are not permeable
and help in creating the negative charge imbalance across the membrane.
Much work has been done on the giant axon of the squid, which has uniquely high intracellular potassium
(400 mM compared to 20 mM outside) and high extracellular fluid sodium (440 mM vs, 50 mM inside) and chloride (560 mM vs 52
mM inside). Mammalian cell concentrations are much lower, but the relative size of the gradient is about the same.
Typical ion concentrations and permeabilities for mammalian membranes.
| Ion |
Cell (mM) |
Blood (mM) |
Permeability (cm/s) |
| potassium |
140 |
5 |
5 x 10-7 |
| sodium |
5-15 |
145 |
5 x10-9 |
| chloride |
4 |
110 |
1 x 10-8 |
| X- (neg. macromol.) |
138 |
9 |
0 |
How can we account for the markedly greater permeabilities of ions (1000x to 1,000,000 x) in mammalian
cell membranes compared to synthetic lipid vesicles? Previously, we showed that glucose has a greater permeability through red blood cell membranes than through synthetic liposomes because of a membrane receptor that allows facilitated diffusion across the membrane and down a concentration gradient. The
same thing is true of ion permeabilites in intact biologicial membranes. These membranes have several types of selective ion
channels (nongated - always open, and gated - open only after specific conformational changes). The nongated
channels dramatically increase the permeability of membranes to ions, as the glucose transport protein increased the permeabilty
to glucose. It turns out that this differential permeability contributes to the transmembrane potential. Ion channels
in nerve and muscle can move ions across the membrane at a rate up to 109/s, which is comparable to kcat
for the best enzymes.
If we envision channels as pores, how can we account for the selectivity of the channel to specific ions.
A larger pore should admit any ion less than a maximal size for the pore, so it is hard to image the nature of the selectivity
filter. Because of this, many people discounted the ideas of channels in favor of a transporter, which would bind the
ion selectivity and then, through conformational changes, move the ion across (much like the Na/K ATPase we discussed in the
previous guide). This model could not, however, account for the incredible rates of ion flux across the membrane.
Selectivity can be accounted for by a channel that contains a narrow opening that acts as an ion sieve. The ion looses
most of its hydration sphere and would form specific interactions with amino acid side chains in the pore region. Such
an interaction would be transient and not too tight since the ion must pass through the membrane. As we will see
later, these ion channels:
- pass ions down a concentration gradient in a thermodynamically favorable process
- are specific for certain ions (although a few are less selective and will pass Na, K, Ca, and Mg ions)
- allow ion flow through either ungated or gated channels.,
- saturate with increasing ion concentration (even through as concentration increases, the ions have a
greater thermodynamic drive to pass through the channel). This is consistent with binding of the ion at a selectivity
filter in the narrow part of the pore. The Kd for the interaction is usually in the mM range and indicates weak binding
with large dissociation rate constants (koff).
The Transmembrane Potential
Several questions arise about the distribution of ions and the magnitude of the transmembrane potential.
- How are the ion gradients established?
- How does the ion distribution contribute to the resting membrane potential?
- How is resting potential and the distribution maintained?
The answer to these questions will be illustrated using studies on two types of brain cells, glial cells
(which function as protectors, scavengers, and feeder for brain neurons) and neurons. Both types of cells have transmembrane
potentials.
Glial Cells
1. The transmembrane ion gradients for ions are initially established through the action of ion-specific
ATPases (P-type ion transporters), such as we discussed with the Na/K ATPase. This transporter ejects 3 sodium ions from the
inside of the cell for every 2 potassium ions in transports in, all against a concentration gradient.
2. The harder question is how the ion distribution contribute to the resting membrane potential.
Two things must occur for a membrane potential to exist: First, there must be a concentration gradient of charged ions
(for example, sodium, potassium, or chloride) across the membrane. Second, the membrane must be differentially permeable
to different ions. If the membrane were completely impermeable to ions, then no movement of ions across the membrane
could occur, and no membrane potential would arise. If, however, membranes are differentially permeable to the
ions, an electrical potential across the membrane can arise. Remember, synthetic bilayers are quite impermeable
to ions, given the hydrophobicity of the internal part of the bilayer. Likewise it is quite impermeable to glucose. It turn
out that glial cells appear to have only a non-gated potassium channel, which allows the outward flow of potassium ions down
the concentration gradient. The inside will then have a net negative charge since impermeable anions remain. The chemical
potential gradient causes this outward flow of potassium ions. As more ions leave, the inside gets more negative, and a transmembrane
potential which resists further efflux of potassium develops. Eventually they balance, and the net efflux of potassium stops.
The resting transmembrane potential reaches -75 mV which is exactly the value obtained from the equations we will derive below.
Since glial cells appear to only express a nongated potassium channel, their resting potential is equal to the potassium equilibrium
potential.
Figure: Visualizing the transmembrane potential in K+ loaded vesicles + a nongated
K+ channel.

How can this equilibrium potential be calculated? The thermodynamic driving force,
DG, for an ion X moving across the membrane (from outside to inside) of transmembrane
potential DY is given by the following equation (where F, the Faraday constant,
= 23,000 cal/V.mol):
DG = [Gin - Gout] + zFDY
This shows that the total driving force for ion movement consists of a chemical potential
(first term) plus an electrical potential (second term). The equation can be expanded and rearranged as follows, where
Xin and Xout are the concentrations of ion X inside and outside the cell, respectively:
DGx = (DGxo
+ RTlnXin) - (DGxo + RTlnXout)
+ zFDY
DGx = RTlnXin - RTlnXout + zFDY
1) DGx = RTln(Xin/Xout)
+ zFDY
2) DGx = 2.303RTlog(Xin/Xout
) + zFDY
Consider K+, where Xin/Xout = 20. (The table above suggests that it is
more like 35, but some texts use the value of 20.) What would the transmembrane potential have to be so that no driving
force would exist for K ions to move across the membrane (i.e. under equilibrium conditions)? Under these conditions,
DGx = 0, so
3). -2.303RTlog(Xin/Xout ) = zFDY
4) -0.0615log(Xin/Xout ) = zDY (at 310K or 37oC)
5) -0.0591log(Xin/Xout ) = zDY
(at 298K or 25oC)
DY is about -0.075 V or -75 mV (assuming
37oC = 310K, R = 1.98 cal/(K.mol), and z =1). That is, since the inside is more negative than
the outside, then K ions would tend to stay inside even if the chemical potential of K ions is greater on the inside. A similar
calculation for Na ions, with a Xin/Xout of about 0.083, gives an equilbrium Na ion potential of about
+55 mV. Why is the actual transmembrane potential close to the equilibrium potential of K ions and not that of Na ions? The
reason has to do with the fact that the permeability of K+ ions is 100 fold greater than of Na ions. Hence
it is the K ions which mostly determine the cell resting potential. (Remember glial cells have only a nongated K channel.)
Equation (1) above (DGx = RTln(Xin/Xout)
+ zFDY) can be solved for DY at
equilbrium and is given by:
DYeq = -(RT/zF)ln(Xin/Xout) which is the Nernst
equation you remember from General and Analytical Chemistry.
In general, the DYeq is determined by more
than one ion (usually Na and K), so the DYeq is between the DYeq for these ions alone. A more general equation can be derived which
shows that the DYeq is determined not only by the concentrations
but also the permeability of these ions. Even with a concentration gradient, if ions could not flow across the membrane,
no membrane potential would arise (assuming electrical neutrality across both sides of the membrane to begin with).
This equation is the Goldman equation and is given by:
DYeq = - (RT/F) ln {[PKK+in + PNaNa+in
+ PClCl-out] / [PKK+out + PNaNa+out + PClCl-in]}
DYeq = - 2.303 (RT/F) log {[PKK+in
+ PNaNa+in + PClCl-out] / [PKK+out
+ PNaNa+out + PClCl-in]}
DYeq (in volts) = - 0.059 log {[PKK+in + PNaNa+in
+ PClCl-out] / [PKK+out + PNaNa+out +
PClCl-in]}
DYeq (in mV) ~ - 59 log {[PKK+in + PNaNa+in
+ PClCl-out] / [PKK+out + PNaNa+out +
PClCl-in]}
where PX is the permeability of ion X. This treatment recognizes the importance of thermodynamics
(chemical and electrical potentials) and kinetics (permeability coefficients). Remember this potential would not be
possible if the ion gradient was not maintained by Na/K ATPase.
Fluorophores that insert into membranes and whose flourescence changes with transmembrane potential have been developed.
An example is di-4-ANEPPS, a AminoNaphthylEthenylPyridinium dye, whose structure is shown below.

When bound to membranes, this probe has an excitation and emission maximum of 475 and 617 nm, respectively.
When the membrane potential is made more negative (hyperpolarized), the fluorescence intensity (excitation 440 nm) decreases
while the emission increases when excited at 530 nm.
Neurons
In the 1940's, ways were developed to measure the actual transmembrane potential of cells. Varying the
outside sodium and potassium concentrations would change the experimental transmembrane potential, as indicated by the Nernst
equation. The experimental resting potentials of glial cells always matched the theoretical potassium equilibrium potentials,
supporting the view that the transmembrane potential was associated only with open, nongated potasisum channels. This was
not observed with neurons, suggesting that channels other than for potassium were open. Using radioactive tracers and potential
measurements, it became clear that nerve cells were permeable not only to potassium, but also to sodium and chloride. How
do these work in establishing the resting potential? Consider the simplest case when just potassium channels are
present, along with an unequal distribution of other ions. Now add some sodium channels. Two forces act to drive sodium into
the cell - the chemical potential since sodium is higher on the outside, and the electrical potential since the inside of
the cell is negative. The equilibrium potential of a cell if it were only permeable to sodium is +55 mv, so there is a great
electrical drive for sodium to enter through the nongated, open sodium pores we just added. As sodium enters, the cell starts
to "depolarize" and have a more positive voltage. However, since in our example, there are many more open potassium channels,
the resting potential deviates only a small amount from the potassium potential, since as the potential becomes more positive,
more potassium flows out down the concentration gradient. Eventually the enhanced potassium efflux equals the sodium influx,
and a new resting membrane potential of -60 mV is established, which is typical of neurons.
3. Now we can answer the last question above: How is the resting potential and the ion distribution
maintained? For a resting potential to be maintained once established, the rate of sodium influx must equal the rate of potassium
efflux through the open, non-gated channels in order to maintain separation of charge across the membrane. However, if influx
and efflux were allowed to continue, the actual ions gradients across the membranes would collapse. This problem is solved
by the Na/K ATPase. In the resting cells, the passive fluxes of sodium and potassium ions are exactly balanced by the active
fluxes of these ions mediated by the Na/K ATPase. The cell is not really at equilibrium but at a steady state.
BINDING OF NEUROTRASMITTER TO RECEPTORS: CELL ACTIVATION
What happens when a neurotransmitter binds to a receptor on the post-synaptic cell? We will study
two examples. The first is the simplest: binding of the transmitter acetylcholine, released by a motor neuron,
to its receptor on muscle. This region is called the neuromuscular junction. Binding of acetylcholine will lead
to a transient depolarization of the muscle cell. Next we will discuss the interaction of a neurotransmitter
with a post-synaptic neuron in the central nervous system. This is a much more complex system. Their differences
are described below:
In neurons interacting with muscles:
- Most muscle fibers are innervated by only one neuron - a motor neuron
- Neurotransmitter release at the neuromuscular junction leads only to muscle excitation, not inhibition.
- All fibers are excited by the same neurotransmitter - acetylcholine.
In the central nervous system, life is more complicated:
- Stimuli are received from hundreds to thousands of different neurons.
- Nerves receive both excitatory and inhibitory stimuli from neurotransmitters
- Different kinds of receptors are present to receive stimuli, which control the activity of different
kinds of channels.
- The ion channels in neurons are gated by a variety of mechanisms in addition to changes in membrane potential,
including gating by heat, cold, stretch, or covalent modification.
- Most nerve cells have a resting potential of about -65 mV compared to a -90 mV for a muscle cell.
Now what happens when a neurotransmitter binds to the receptor on the post-synaptic cell? A depolarization
occurs (mediated by conformational changes in the transmitter-receptor complex) raising the membrane potential from the resting
equilibrium level. What happens next depends on the identity of the post synaptic cell. In the muscle cell, the
rising potential caused by binding of acetylcholine ultimately leads to muscle contraction by opening calcium channels.
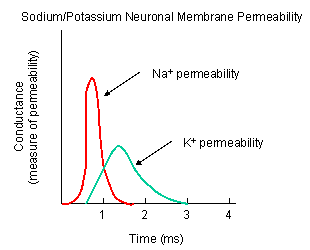
In a neuron, the rising potential triggers an action potential by opening voltage-gated sodium channels. The potential
rises to about + 35 mV, but does not reach the Na ion equilibrium potential, because the high positive potential opens a voltage-gated
potassium channel. The potential then falls until it reaches the K ion equilibrium potential where the cells is hyperpolarized.
It slowly then relaxes back to the resting potential of -60 mV. This wave of changes in potential sweeps down the post-synaptic
cell membrane and is the basis for the "firing" of the neuron.
Figure: DEPOLARIZATION OF TRANSMEMBRANE POTENTIAL
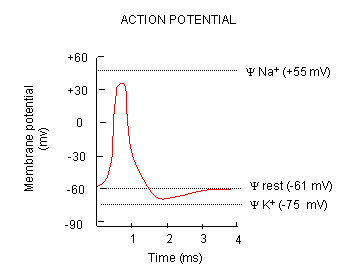
Figure: NA AND K PERMEABILITIES DURING DEPOLARIZATION
THE PROTEIN PLAYERS
We must now account for the rise and fall of the membrane potential to a variety of neurotransmitters,
including the cholineric transmitters (ex. acetylcholine), catecholamines (dopamine, epinephrine, norepineprine), amino acid
derivatives (ex. Glu, Asp, N-methyl-D-Asp, Gly, gamma-amino-butyric acid -GABA), and peptides (endorphins, encephalins). We
will consider five membrane proteins:
Figure: five membrane proteins
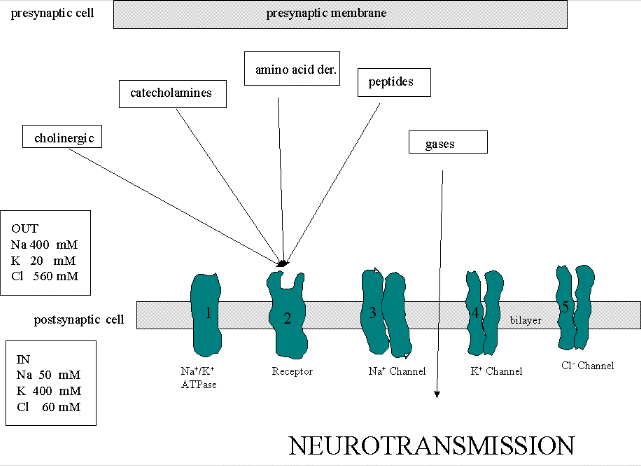
- Na+-K+-ATPase: We discussed this in the previous study guide on active
transport. It transports both sodium and potassium ions against a concentration gradient using ATP as an energy source. The
protein is a sodium dependent ATPase. Without this protein, the membrane potential could not be maintained since the
sodium and potassium gradient would collapse. It also contributes to the potential since its is an electrogenic antiporter.
(In addition, we have seen that ungated potassium and sodium channels are also present.)
- Neurotransmitter receptor: The receptors we will consider here are typically ligand-gated
ion channels. Once ligand binds, a conformational change occurs in the protein, allowing a flow of ions down a concentration
gradient. Depending on the nature of the ion, the channel either initiates depolarization (when Na+ enters from
the outside and raises DY) or inhibits depolarization (when Cl-
enters from the outside and lowers DY). When chloride channels open,
they hyperpolarize the transmembrane potential. Stimulatory neurotransmitters (like glutamate) lead to depolarization
of the membrane, while inhibitory neurotransmitters (like gamma-aminobutyric acid) lead to hyperpolarization of the membrane
(make the potential more negative).
- Na+ channel (voltage-gated): When the ligand-gated channel depolarizes the membrane
to some threshold value, sodium channels undergo a conformational change and open allowing Na+ ions to flood into
the cell, raising the potential to a positive approx. 33 mV (a value lower than the the equilibrium sodium potential). This
membrane protein is a voltage-gated channel, not a ligand gated one. Somehow, it senses a change in the transmembrane potential
initiated by opening of the ligand-gated channel.
- K+ channel (voltage gated): When the membrane potential reaches around +25 mV
or so, the K+ channel, a voltage-gated membrane protein, alters its conformation, allowing K+ efflux
from the cells, lowering the potential until it reaches the potassium equilibrium potential. It slowly relaxes back to the
cell resting potential of about -60 mV. Recently, the crystal structure of the K+ channel from Streptomyces
lividans was determined (Science, 280, 69-77, 1998): "All K+ channels show a selectivity
sequence of K+, Rb+ > Cs+, whereas permeability for the smallest alkali metal ions Na+
and Li+ is immeasurably low. Potassium is at least 10,000 times more permeant than Na+, a feature that
is essential to the function of K+ channels.....Two aspects of ion conduction by K+ channels have tantalized
biophysicists for the past quarter century. First, what is the chemical basis of the impressive fidelity with which the channel
distinguishes between K+ and Na+ ions, which are featureless spheres of Pauling radius 1.33 Å and 0.95
Å, respectively? Second, how can K+ channels be so highly selective and at the same time, apparently paradoxically,
exhibit a throughput rate approaching the diffusion limit? The 104 margin by which K+ is selected over
Na+ implies strong energetic interactions between K+ ions and the pore. And yet strong energetic interactions
seem incongruent with throughput rates up to 108 ions per second."
- Cl- channel: If these channels (typically ligand-gated) are open, they will
hyperpolarize the cell and make it more difficult to fire.
A MORE DETAILED LOOK AT THE IMPORTANT PROTEINS
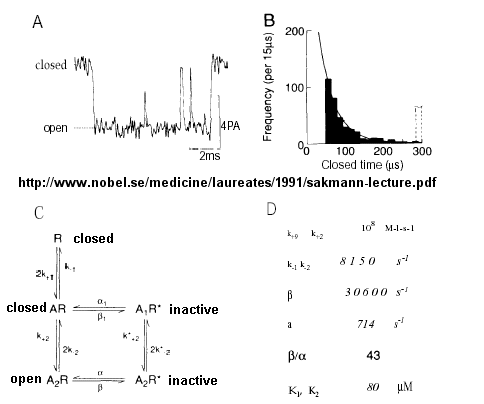
- The Ligand-gated Acetylcholine Receptor at the Neuromuscular junction - Kinetic modeling
based on patch-clamp recordings show that the protein can exists in multiple conformations, including a closed (C), open (O),
and inactive (I) forms. The binding of two acetylcholine molecules is required to open the channel. When two are bound, the
protein exist in two interconvertible forms: A2C <==> A2O. Through another conformation change,
the open form O can inactivate in a slow step to A2I, where I is an inactive form.
The channel consists of five
helices which are constricted by hydrophobic side chains which point inward into the pore. A rotation and sliding of the helices
relative to each other probably occurs when ligand binds the protein, allowing the channel opening to increase. Rings of negatively
changed side chains line the pore at the top and bottom accounting for the selectivity of the channel for positive ions.
Much of our understanding of the mechanism of the acetylcholine channel opening comes from a patch clamp
technique in which a micropipette is used to remove a small section of a membrane containing a channel.
Figure: patch clamp technique
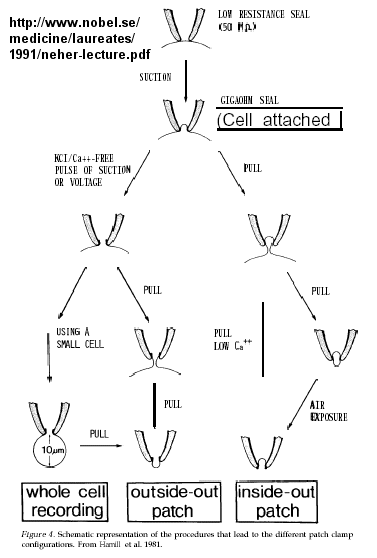
Ion flow, measured as picoamp current, can be measured across the membrane patch. The opening and
closing of single channels can be recorded using this technique, for which Nehert and Sakman won the Nobel Prize.
Figure: opening and closing of single channels
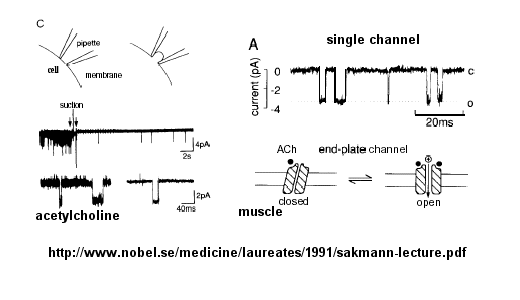
From this, they deduced a mechanism for gating of the acetylcholine channel.
Figure: mechanism for gating of the acetylcholine channel
In general, transmitter-gated channels are similar to the acetylcholine receptor. Mechanisms to
generate an excitatory synaptic potential (with a transmitter-gated receptor/channel) are similar to that of generating an
action potential (with voltage-gated channels) in that both involve movement of sodium and potassium ions across the membrane.
They differ in several ways, however:
- In the generation of action potentials, sodium and potassium ions move through different voltage-gated
channels - i.e. the channels are selective for the ion. Transmitter-gated channels usually are not selective for the ions
since the pore is too large.
- ion flux through voltage-gated channels is "regenerative" in that increased depolarization caused by
the channel opening leads to more influx of the ion. In transmitter-gated channel, the amount of ion passing through the membrane
depends on the local concentration of neurotransmitter released at the synapse.
- When acetylcholine causes the opening of the acetylcholine receptor/pore, sodium can flow in and potasium
can flow out (down their respective concentration gradients). However, more sodium flows in initially than potassium flows
out since potassium efflux is resisted by the negative transmembrane potential. This leads to an inward flow of sodium enough
to cause the activation of potential-gated sodium channels. Since these are voltage gated, much more sodium can enter
the cell, leading to an action potential and the ultimate opening of vesicular calcium ion channels. This leads to a
rise in intracellular calcium (through opening of a Ca channel in membranes of intracellular organelles with high concentrations
of Ca ions), which activates muscle contraction.
- Neuromuscular Junction
- Electron Micrograph of Junction-End Plate
- The Sodium Channel - Patch clamp recordings of the sodium channel reconstituted in vesicles
shows it to be a voltage-gated channel. Two potent neurotoxins, tetrodotoxin (from Puffer fish) and saxitoxin bind to the channel and act as antagonist (inhibits the activity of the receptor by blocking sodium influx).
Figure: Puffer fish

The guanidino group of the tetrodotoxin appears to bind with high affinity to the entrance of the channel
that interacts with the hydrated sodium ion. Affinity chromatography using tetrodoxin beads have been used to
purify the protein. The protein sequence consists of 4 repeating units, each containing 6 transmembrane helices. Ion selectively
of the sodium channel is determined by the size of the the ion when it is hydrated by one water molecule.
Figure: Ion selectively of the sodium channel
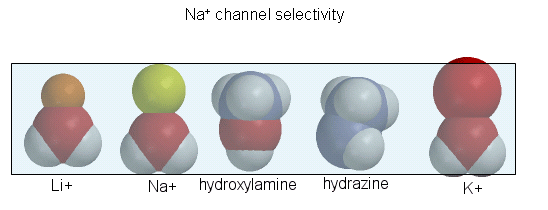
Hence Li and Na ions can pass through, but not the large K ion. Hydroxylamine and hydrazine both have
the same width as a water-Na+ complex, and are both positively charged. These can also pass through the channel.
At the narrowest part of the channel a water (and presumably the hydroxylamine and hydrazine) form H-bonds to side chains
in the pore while the positive charge on the ion forms transient salt-bridges to either a Glu as Asp in the pore. The open
channel can likewise spontaneously inactivate by undergoing another conformational change. Comparison of the sequence of this
channel with calcium and potassium channels show extensive sequence and structural similarities. One of the 6 transmembrane
helices, S4, appears to be the voltage sensor. Depolarization of the membrane potential rmay result in an outward movement
and rotation of the positively charged helixes containing Lys and Arg side chains which had presumably formed salt-bridges
with negatively charged side chains within the protein. Depolarization of the membrane results in breaking a few salt bridges,
and effectively leads to the movement of 1 or 2 charges on the helix through the membrane. Work occurs when charges are moved
through an electric field. Work is also related to the DG for the system,
which is also dependent on the ratio of the open and closed form of the channel. Other voltage-gated ion channels (for potassium
and chloride) have a similar membrane topology and an S4 voltage-sensor helix.
- The Potassium Channel - How can the two essential features of the K+ channel
pore - selectivity for the larger potassium ion over the sodium ion, and the near diffusion-limited rate of potassium ion
flux through the channel be reconciled?
Figure: Electrostatics of the K+ channel .

The selectivity filter is composed of many stacked rings of oxygens that can interact with
a dehydrated K ion but not with a dehydrated Na ion which can not approach close enough to form significant interactions.
Surrounding the filter are twelve aromatic amino acids which constrain the size of the pore opening. The interactions
of the filter O's with the K ion makes up for the energetically disfavored dehydration of the ion. The filter
contains two K ions which repel each other, assisting in the vectorial discharge of the ions through the membrane.
These ions must have form weak interactions with the selectivity filter. The actual pore is mostly hydrophobic, which
facilitates flow-through of the ions. The central cavity of the pore can hold some waters molecules in addition
to the K ions which helps stabilize the ion in the middle of the pore.
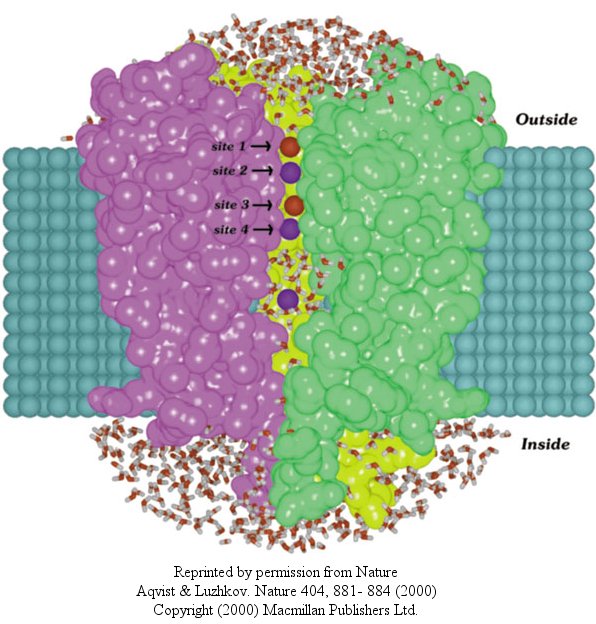
In another recent paper (Nature, 404, April 20, 2000, 881-884), molecular dynamic calculation
were performed to distinguish between various models for binding and selectivity of the channel. They found the favored
conduction pathway arises from conformational changes between 2 discrete shapes that differ in energy by only about 5 kcal/mol
(about 1-2 H bonds). The picture below shows the channel with one of the 4 subunits removed for clarity. Water
is shown in red and the K ions in blue. Two ions are in the filter and one in the middle cavity.
Figure: K+ Channel from Steptomyces lividans
MacKinnon's laboratory (2003) has recently determined the X-ray structure of a voltage-dependent K+ channel
from Aeropyrum pernix, an archaebacteria. This protein is homologous to eukaryotic K+ channels.
This membrane protein was solubilized with detergent and crystallized in the presence of an antibody which inhibited the flexibility
of part of the protein, facilitating the formation of crystals. Like the sodium channel, this protein has 4 subunits
each consisting of a 6 alpha-helices which cross the membrane. The S4 helix, which has multiple positively charged side
chains, is present in each subunit and acts as a voltage sensor. It was presumed that the helices would would
twist in a ratchet-like fashion, leading to the movement of positive charge in the S4 helix across the membrane (as described
above for the Na channel). MacKinnon's group found evidence for another mechanism for voltage sensing. Crystal
structures show that the S4 helices is imbedded in the membrane, and is not interacting directly with other parts of the protein.
It forms an alpha-helical haripin (a paddle shape) which can move through the membrane on change of the transmembrane potential.
The topological disposition of paddle (within the membrane) explains the effect of small, lipophilic molecules (like anesthetics
nerve toxins, insecticides like DDT) on the channel. His group also labeled the S4 helix with a biotin-17 angstrom
linker complex. On change of the transmembrane potential the biotin flips from across the membrane where it can bind
to (and be detected by) its natural binding partner, avidin. The authors suggest that the "voltage sensitive paddles
operate somewhat like hydrophobic cations attached to levers, enabling the membrane electric field to open and close the pore."
Figure; S4 paddle voltage sensor of the voltage-dependent K+ channel from Aeropyrum pernix

Channels, once open, must be inactivated. In the case of the voltage-gated potassium channel, inactivation occurs
when the amino-terminal cytoplasmic domain binds to the potassium pore on the cytoplasmic side, in interaction likened to
the binding of a "ball on a chain" (the cytoplasmic domain) to the pore opening. The chain acts to tether the ball domain
so it may swing to bind to the pore opening. The ball domain contains both positively charged and hydrophobic regions.
Where is the ball domain in the absence of inhibition? Recent studies (Oliver et al.) have shown that e positive domain
can bind to proximal phosphatidyinositol 4,5-bisphosphate (PIP2) lipids on the inner leaflet of the membrane bilayer.
When so bound, inactivation of the channel is prevented. As you will see in the next section, PIP2 can also
be cleaved to form diacylglycerol and inositol 1,4,5-trisphosphate when cells are activated byexternal factors (hormones,
growth factors, etc) in the process of signal transduction.
Alcohol and Neurons
Alterations of potasium channel has recently been implicated in the inhibitory effects of ethanol. Davies,
McIntire, et al. studied effects of ethanol on he round worm C. elegans, believing that alcohol-mediated inhibition
of neural activity would be conserved across species. Previously it has been shown that the dose-effect curves for behavioral
changes is similar for both invertebrates and vertebrates. Ethanol seems to affect many different proteins that would
lead to synaptic inhibition, including GABA and glutamate channels and potassium channels. Many different gene products
(dopamine D4 receptors, protein kinase C) are associated with increased sensitivity while others (nitric oxide synthase, dopamine
D2) are associated with ethanol resistance. These changes suggests the complex pathways are involved in ethanol effects
but don't isolate a specific target for its effects.
When C. elegans were exposed to ethanol for brief time periods, ethanol levels rose to values similar
to levels seen in intoxicated drivers (0.1%). The isolated mutants that were resistant to ethanol effects (changes in
movement and egg-laying behavior). These mutants affected a single gene, slo-1, homologous to the the slowpoke gene
in drosophila. The gene in both organisms encoded a BK potassium channel, whose normal function is to repolarize neural
membranes. Mutants strains, when transformed with slo-1+ regained ethanol sensitivity. Ethanol appears to directly activate
the channel. This would lead to efflux of potassium ions from the worm, hyperpolarizing the neural cells, leading to
inhibition of neural activity. Effects in C. elegans were observed at physiologically relevant ethanol, ranging from
those that produce euphoria to sedation in humans.
Excitatory Neurotransmitters in the Brain:
Glutamate is a major excitatory neurotransmitter in the brain. Four types of glutamate receptors are found
in the central nervous system. They differ in the nature of ligands which bind to the receptor and which act as agonists.
Figure:
Excessive amounts of glutamate are neurotoxic. Three are described below:
- AMPA receptor, which binds a-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid and acts as a sodium and potassium
ion channel.
- Kainate receptor, named after the molecule kainate which acts as an agonist. This is a sodium and
potassium ion channel.
- NMDA (N-methyl-D-Asp) receptor, which allows flow of sodium, potassium
and calcium, and is regulated by glycine and Zn2+. The street drug PCP (phencyclidine) inhibits this
channel.
Inhibitory Neurotransmitters:
The main inhibitory neurotransmitters are GABA (gamma-aminobutyric acid, which is made from Glu through
decarboxylation of the a-C group) and glycine. The bind to transmiitter-gated
chloride channels, which when open hyperpolarize the membrane. Benzodiazepines (like Valium and Librium - anti-anxiety and
muscle-relaxing agents) and barbituates (like phenobarbital-hypnotics) bind at allosteric sites and potentiate the binding
of each other and GABA.
Figure: Mechanisms of Channel Gating
Summary:
1. the same ions moving through different channels can have different consequences. Consider the example
of potassium ions. When it moves through a:
- nongating channel, it establishes the resting potential
- a voltage gated channel, it repolarizes the cell after an action potential
- channel that is gated by chemical modification (such as phosphorylation), it may hyperpolarize the membrane
(make it more negative inside) and facilitate neuron inhibition
2. If two ions are involved in signaling, the result depends on
- if the two species move simultaneously through the same channel (which results in excitation through
an initial depolarization of membrane if the ions are potassium and sodium)
- if the two species move through different channels in a sequential fashion (which generates an action
potential) if the ions are potassium and sodium).
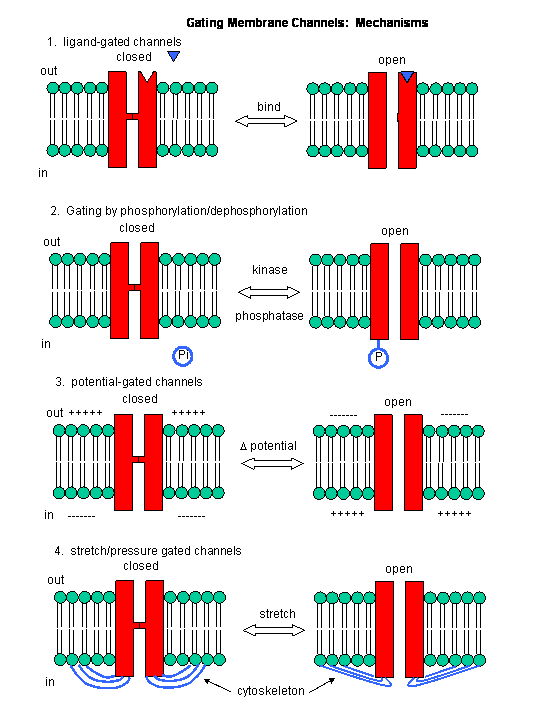
In summary, ligand and voltage gated channels allow changes in the polarization of the membrane. Other
mechanisms can also lead to changes. Membrane proteins can be phosphorylated (using ATP) by protein kinases in the cell, leading
to a change in the conformation of the membrane protein, and either an opening or closing of the channel. Channels linked
to the cytoskeleton of the cells can also be opened or closed through stretching. Other stimuli that gate channels are light
(through photoisomerization-induced conformational changes), heat, and cold.
 Literature Online Literature Online
Ion channel genes and human neurological disease: Recent progress, prospects, and challenges by Edward C. Cooper and Lily Yeh Jan. PNAS, Vol. 96, Issue 9, 4759-4766, April 27, 1999
|

