HOW TO CALCULATE DG^O FROM PROTEIN DENATURATION CURVES:

Multiple methods can be used to investigate the denaturation of a protein. These include UV, fluorescence, CD, and viscosity measurement. In all these methods the dependent variable (y) is measured as a function of the independent variable, which is often temperature (for thermal denaturation curves) or denaturant (such as urea, guanidine hydrochloride) concentration. From these curves we would like to calculate the standard free energy of folding or unfolding (DG^O) for the protein (for the reaction N <=> D). The denaturation curves usually show a sigmoidal, cooperative transition from the native to the denatured state. The dependent variable can also be normalized to show fractional denaturation (f_D). Example of these curves are shown in the figure below:

Figure:  DENATURATION CURVES FOR PROTEINS

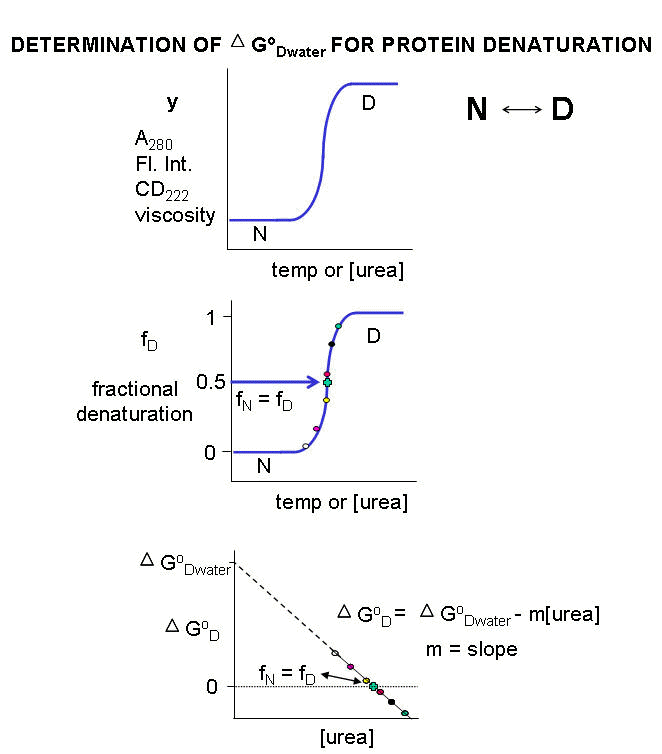
For each curve, the value of y (either A₂₈₀, Fluorescence intensity, viscosity, etc) can be thought of as the sum contributed by the native state and from the denatured state, which are present in different fractional concentrations from 0 - 1. Hence the following equation should be reasonably intuitive.

1. y = f_N y_N + f_D y_D where f_N is the fraction native and y_N is the contribution to the dependent variable y from the native state, and f_D is the fraction denatured and y_D is the contribution to the dependent variable y from the denatured state. Conservation give equation 2.

2. 1 = f_N + f_D or f_N = 1 - f_D. Substituting 2 into 1 gives:

• y = ( 1 - f_D) y_N + f_D y_D .
• y = y_N - f_Dy_N + f_D y_D .
• y - y_N = f_D (y_D - y_N). Rearranging this equation gives

3. f_D = (y - y_N) / (y_D - y_N)

Notice the right hand side of the equations contains variables that are easily measured.

By substituting 2 and 3 into the expression for the equilibrium constant for the reaction N<=> D we get:

K_eq = [D]_eq/[N]_eq = f_D/f_N or

4. K_eq = f_D/(1 - f_D) and

5. DG^o = -RTlnK_eq = -RTln[ f_D/(1 - f_D)]

Remember that DG^O  (and hence K_eq) depends only on the intrinsic stability of the native vs denatured state for a given set of conditions.  They vary as a function of temperature and solvent conditions.  At low temperature and urea/guanidine HCl concentration, the native state is favored, and for the N <=> D transition,  DG^O  < 0.  At high  temperature and urea/guanidine HCl concentration, the denatured state is favored, and  DG^O  > 0.  tAt some value of temperature or urea/guanidine concentration, both the native and denatured state would be equally favored.  At this point, Keq = 1 and DG^O  = 0. cIf temperature is the denaturing agent, the temperature at this point is called the melting point (Tm) of the protein, which is analogous to the Tm (in the heat capacity vs temperature graphs) for the gel to liquid crystalline phase transition of phospholipid vesicles. 

Figure:  gel to liquid crystalline phase transition of phospholipid vesicles

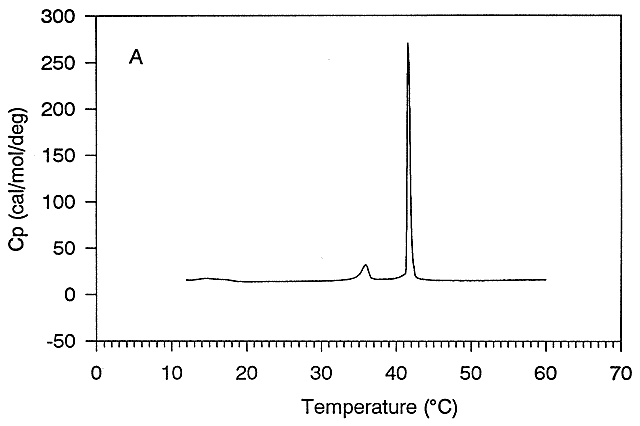
Ordinarily, at a temperature much below the Tm for the protein, so little of the protein would be in the D state that it would be extremely difficult to determine the concentration of the protein in the D state. Hence it would be difficult to determine the K_eq or DG^o for the reaction N <=> D. However, in the range where the protein denatures (either with urea or increasing temperature), it is possible to measure f_D/f_N.and hence D G^o at each urea or temperature. A plot of DG^o vs [urea] is linear, and by extrapolating the line to [urea] = 0, the D G^o_w, the free energy for denaturation of the protein in water, can be estimated. (See above figure.) The same method is not usually used when increasing temperature is the denaturant since D G⁰ for protein folding usually changes with T (remember the D Cp for protein unfolding).